题目内容
已知双曲线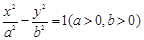 ,
,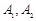 为实轴顶点,
为实轴顶点,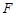 是右焦点,
是右焦点,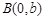 是虚轴端点,
是虚轴端点,
若在线段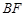 上(不含端点)存在不同的两点
上(不含端点)存在不同的两点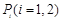 ,使得
,使得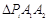 构成以
构成以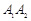 为斜边的
为斜边的
直角三角形,则双曲线离心率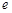 的取值范围是( )
的取值范围是( )
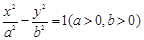 ,
,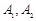 为实轴顶点,
为实轴顶点,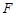 是右焦点,
是右焦点,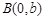 是虚轴端点,
是虚轴端点,若在线段
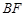 上(不含端点)存在不同的两点
上(不含端点)存在不同的两点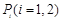 ,使得
,使得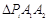 构成以
构成以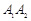 为斜边的
为斜边的直角三角形,则双曲线离心率
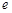 的取值范围是( )
的取值范围是( )A.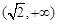 | B.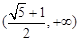 | C.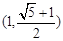 | D.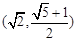 |
D
试题分析:由题意知,要使得在线段
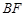 上(不含端点)存在不同的两点
上(不含端点)存在不同的两点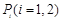 ,使得
,使得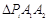 构成以
构成以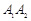 为斜边的直角三角形,只需以
为斜边的直角三角形,只需以 为直径的圆与线段
为直径的圆与线段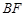 相交于两点,且端点不是交点即可,故圆心
相交于两点,且端点不是交点即可,故圆心 到直线
到直线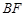 的距离
的距离 满足
满足 ,即
,即 ,解得
,解得 ,故
,故

练习册系列答案
相关题目
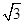 ,则C的实轴长为( )
,则C的实轴长为( )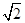
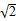 )上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
)上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.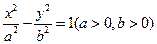 的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF1⊥AF2,原点O到直线AF1的距离为
的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF1⊥AF2,原点O到直线AF1的距离为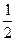 |OF1|,则双曲线的离心率为( )
|OF1|,则双曲线的离心率为( )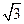 +1
+1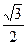

 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
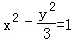 的渐近线的距离是( )
的渐近线的距离是( )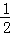
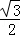

 的右焦点F,作圆x2+y2=a2的切线FM交y轴于点P,切圆于点M,
的右焦点F,作圆x2+y2=a2的切线FM交y轴于点P,切圆于点M, ,则双曲线的离心率是( )
,则双曲线的离心率是( )


 的离心率为
的离心率为 ,一个焦点与抛物线
,一个焦点与抛物线 的焦点相同,则双曲线的渐近线方程为( )
的焦点相同,则双曲线的渐近线方程为( )



 为C的实轴长的2倍,则C的离心率为
为C的实轴长的2倍,则C的离心率为
