题目内容
对于△ABC内的任何一点M,为了确定M的具体位置f(M),采用如下记法:f(M)=(x,y,z),x,y,z分别表示△MBC,△MCA,△MAB的面积,现有△ABC满足 •
• =
= 且∠A=30°,设M是△ABC内的一点(不在边界上),当
且∠A=30°,设M是△ABC内的一点(不在边界上),当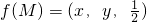 ,那么
,那么 的最小值为________.
的最小值为________.
18
分析:由向量的数量积公式得| |•|
|•| |•cos∠BAC=2
|•cos∠BAC=2  ,从而|
,从而| ||
|| |=4,再由题意得x+y的值,最后利用“1的代换”化简,结合基本不等式求最值即可得答案.
|=4,再由题意得x+y的值,最后利用“1的代换”化简,结合基本不等式求最值即可得答案.
解答:∵ •
• =
= ,∠BAC=30°,
,∠BAC=30°,
所以由向量的数量积公式得| |•|
|•| |•cos∠BAC=2
|•cos∠BAC=2  ,
,
∴| ||
|| |=4,
|=4,
∵S△ABC= |
| |•|
|•| |•sin∠BAC=1,
|•sin∠BAC=1,
由题意得,x+y=1- =
= .
.
∴ =2(
=2(  +
+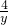 )(x+y)=2(5+
)(x+y)=2(5+ +
+ ≥2(5+2
≥2(5+2  )=18,
)=18,
等号在x= ,y=
,y= 取到,所以最小值为18.
取到,所以最小值为18.
故答案为:18.
点评:本题考查基本不等式的应用和向量的数量积,解题时要认真审题,注意公式的灵活运用,属于中档题.
分析:由向量的数量积公式得|
 |•|
|•| |•cos∠BAC=2
|•cos∠BAC=2  ,从而|
,从而| ||
|| |=4,再由题意得x+y的值,最后利用“1的代换”化简,结合基本不等式求最值即可得答案.
|=4,再由题意得x+y的值,最后利用“1的代换”化简,结合基本不等式求最值即可得答案.解答:∵
 •
• =
= ,∠BAC=30°,
,∠BAC=30°,所以由向量的数量积公式得|
 |•|
|•| |•cos∠BAC=2
|•cos∠BAC=2  ,
,∴|
 ||
|| |=4,
|=4,∵S△ABC=
 |
| |•|
|•| |•sin∠BAC=1,
|•sin∠BAC=1,由题意得,x+y=1-
 =
= .
.∴
 =2(
=2(  +
+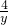 )(x+y)=2(5+
)(x+y)=2(5+ +
+ ≥2(5+2
≥2(5+2  )=18,
)=18,等号在x=
 ,y=
,y= 取到,所以最小值为18.
取到,所以最小值为18.故答案为:18.
点评:本题考查基本不等式的应用和向量的数量积,解题时要认真审题,注意公式的灵活运用,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目