题目内容
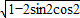等于（ ）A．sin2-cos2
B．cos2-sin2
C．±（sin2-cos2）
D．sin2+cos2
【答案】分析：由2的范围，得到sin2大于0，cos2小于0，进而确定出sin2-cos2大于0，将所求式子中的“1”利用同角三角函数间的基本关系化为sin22+cos22，利用完全平方公式及二次根式的化简公式化简，即可得到结果．
解答：解：∵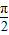
＜2＜π，
∴sin2＞0，cos2＜0，即sin2-cos2＞0，
则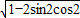
=
=
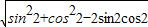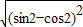=|sin2-cos2|=sin2-cos2．
故选A
点评：此题考查了同角三角函数间的基本关系，完全平方公式，以及二次根式的化简，熟练掌握基本关系及公式是解本题的关键．
解答：解：∵
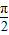＜2＜π，∴sin2＞0，cos2＜0，即sin2-cos2＞0，
则
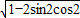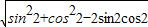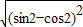===|sin2-cos2|=sin2-cos2．故选A
点评：此题考查了同角三角函数间的基本关系，完全平方公式，以及二次根式的化简，熟练掌握基本关系及公式是解本题的关键．
练习册系列答案
相关题目
,
)，则
等于 ( )
sin(
+
) B．
sin(
-
)
sin(
+
)2 D．
sin(
-
)
B.
D．2sin 
-
等于（ ）
sin（
）
sin（
）
sin（
）
sin（
）
=（-3，2）平移后得到y=sin2x的图象，则f（x）等于（ ）