Question

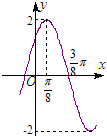（2012•安徽模拟）函数f(x)=2sin(ωx+?)(ω＞0，0＜?＜

π

2

)的部分图象如图所示．
（I）求ω，?的值；
（II）在△ABC中，a=

2

，b=1，f(

A

2

)=-

6

5

，求sinB的值．

Answer 1

分析：（I）由已知根据五点作图法可得最高点与最低点满足的关系，可求ω，∅
（II）由（I）可求f（x），由f（

1

2

A）=-

6

5

可求sin（A+

π

4

），进而可求cos（A+

π

4

），联立可求sinA，再由正弦定理可求sinB

解答：解：（I）由已知可得，

π 8 ω+?= π 2 3 8 πω+?=π

⇒

ω=2 ?= π 4

；                  …（4分）
（II）由（I）知f(x)=2sin(2x+

π

4

)
由f(

A

2

)=-

6

5

⇒sin(A+

π

4

)=-

3

5

…①
∴A+

π

4

∈(

π

4

，

5

4

π)，而sin(A+

π

4

)＜0，
∴A+

π

4

∈(π，

5

4

π)
从而cos(A+

π

4

)=-

4

5

…②
由①②⇒

cosA+sinA=- 3 5 2 cosA-sinA=- 4 5 2

⇒sinA=

2

10

由

a

sinA

=

b

sinB

⇒sinB=

1

10

．…（12分）

点评：本题考查三角函数的解析式的求法，三角函数的图象的应用，考查视图能力与计算能力．