Question

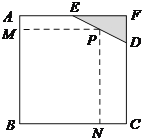
【题目】如图所示，四棱锥的底面是边长为1的菱形，，

E是CD的中点，PA底面ABCD，．

（I）证明：平面PBE平面PAB；

（II）求二面角A—BE—P和的大小．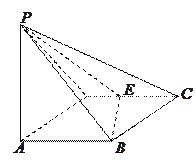

Answer 1

【答案】（I）同解析（II）二面角的大小为

【解析】

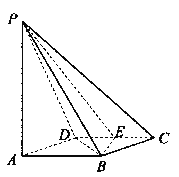
解：解法一（I）如图所示, 连结由是菱形且知，

是等边三角形. 因为E是CD的中点，所以

又所以

又因为PA平面ABCD，平面ABCD，

所以而因此平面PAB.

又平面PBE，所以平面PBE平面PAB.

（II）由（I）知，平面PAB,平面PAB, 所以

又所以是二面角的平面角．

在中,．

故二面角的大小为

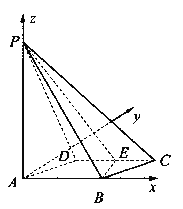
解法二：如图所示,以A为原点，建立空间直角坐标系．则相关各点的坐标分别是

（I）因为平面PAB的一个法向量是所以和共线.

从而平面PAB. 又因为平面PBE，所以平面PBE平面PAB.

（II）易知设是平面PBE的一个法向量,

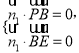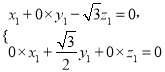则由得所以

故可取而平面ABE的一个法向量是

于是,．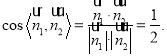

故二面角的大小为