题目内容
在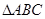 中,
中, 为
为 边上的点
边上的点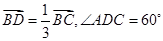 ,且
,且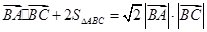 .
.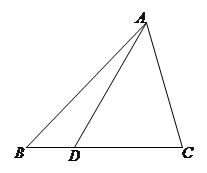
(1)求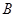 ;
;
(2)若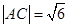 ,求
,求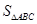 .
.
(1)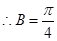 (2)
(2)
解析试题分析:解:(1)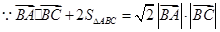 ,
,
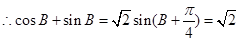

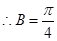
(2)设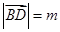 ,则
,则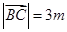 ,在
,在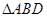 中由正弦定理得
中由正弦定理得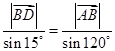
则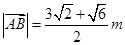 ,
,
在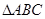 中由余弦定理得
中由余弦定理得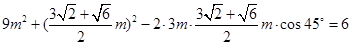
解得 ,
,
则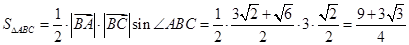
考点:向量的数量积;正弦定理;三角形的面积公式
点评:解三角形的题目,必用到正弦定理、余弦定理和三角形面积公式,有时要结合到向量的性质和三角恒等变换。

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
题目内容
在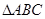 中,
中, 为
为 边上的点
边上的点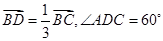 ,且
,且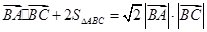 .
.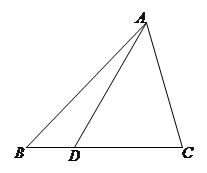
(1)求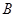 ;
;
(2)若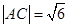 ,求
,求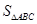 .
.
(1)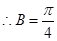 (2)
(2)
解析试题分析:解:(1)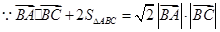 ,
,
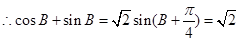

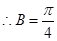
(2)设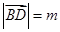 ,则
,则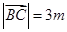 ,在
,在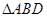 中由正弦定理得
中由正弦定理得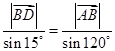
则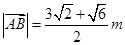 ,
,
在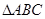 中由余弦定理得
中由余弦定理得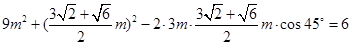
解得 ,
,
则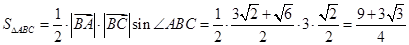
考点:向量的数量积;正弦定理;三角形的面积公式
点评:解三角形的题目,必用到正弦定理、余弦定理和三角形面积公式,有时要结合到向量的性质和三角恒等变换。

 天天向上口算本系列答案
天天向上口算本系列答案