题目内容
用半径为R的圆铁皮剪一个内接矩形，再将内接矩形卷成一个圆柱（无底、无盖），问使矩形边长为多少时，其体积最大？
解：可设矩形的两边x，y，由几何关系x2+y2=4R2故有y=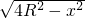
．，
则体积V=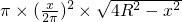
=
∴V′=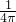
×（2x×+
）
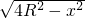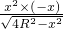令V′=0得2x×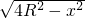+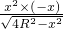=0，整理得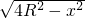=x，解得x=
R，此时另一边长为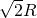
即当x=R时，体积取到最大值，最大值为V=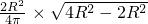
=
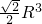
即当长与宽都是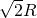时，此圆柱体体积取到最大值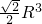
分析：首先分析题目要求半径为R的圆铁皮剪一个内接矩形，将内接矩形卷成一个圆柱（无底、无盖），求其体积最大．故可以设矩形的两边x，y．然后列出方程．由几何关系x2+y2=4R2故有y=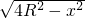．利用公式表示成圆柱体的体积，利用导数求最值即可．
点评：此题主要考查导数求最值在实际中的应用问题，由导数求最值在高考中属于重要考点，需要同学们理解记忆．
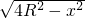．，则体积V=
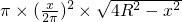=∴V′=
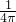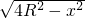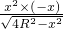×（2x×+）令V′=0得2x×
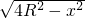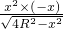+=0，整理得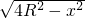=x，解得x=R，此时另一边长为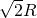即当x=
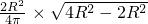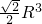
R时，体积取到最大值，最大值为V==即当长与宽都是
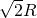时，此圆柱体体积取到最大值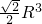分析：首先分析题目要求半径为R的圆铁皮剪一个内接矩形，将内接矩形卷成一个圆柱（无底、无盖），求其体积最大．故可以设矩形的两边x，y．然后列出方程．由几何关系x2+y2=4R2故有y=
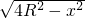．利用公式表示成圆柱体的体积，利用导数求最值即可．点评：此题主要考查导数求最值在实际中的应用问题，由导数求最值在高考中属于重要考点，需要同学们理解记忆．
练习册系列答案
相关题目
B．
C．
D．