题目内容
如图所示,在四棱锥P—ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角.
(1)若AE⊥PD,E为垂足,求证:BE⊥PD;
(2)求异面直线AE与CD所成角的大小(用反三角函数表示).
(1)证法一:∵PA⊥平面ABCD,∴PA⊥AB.
再由AB⊥AD,得AB⊥平面PAD.∴AB⊥PD.
又∵AE⊥PD,∴PD⊥平面ABE.
故BE⊥PD.
证法二:由题设AB⊥AD,AB⊥AP,
∴AB⊥平面PAD.
又AE⊥PD,∴BE⊥PD.
(2)解:如图所示,以A为原点,AB、AD、AP所在直线为坐标轴建立空间直角坐标系,则点C、D的坐标分别为(a,a,0)、(0,2a,0).

∵PA⊥平面ABCD,∠PDA是PD与底面ABCD所成的角,
∴∠PDA=30°.
于是,在Rt△AED中,由AD=2a,得AE=a.
过E作EF⊥AD,垂足为F,
在Rt△AFE中,由AE=a,∠EAF=60°,得
AF=![]() a,EF=
a,EF=![]() a.
a.
∴E(0,![]() a,
a,![]() a).
a).
于是![]() =(0,
=(0,![]() a,
a,![]() a),
a),![]() =(-a,a,0).
=(-a,a,0).
设![]() 的夹角为θ,则由
的夹角为θ,则由
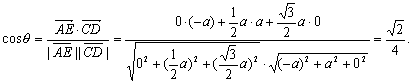
∴θ=arccos![]() .
.
绿色通道:
求一对异面直线所成的角:一是按定义平移转化为两相交直线的夹角;二是在异面直线上各取一向量,转化为两向量的夹角或其补角.无论哪种求法,都应注意角的范围的限定.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
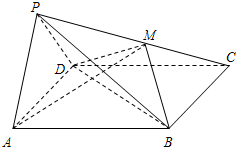 如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.
如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.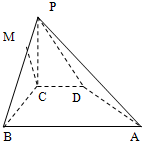 如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角. (2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
(2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE. 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点.
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点. 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB