Question

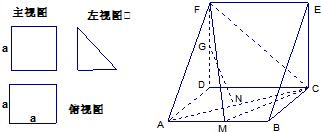一个棱柱的直观图和三视图（主视图和俯视图是边长为a的正方形，左视图是直角边长为a的等腰三角形）如图所示，其中M、N分别是AB、AC的中点，G是DF上的一动点．
（Ⅰ）求证：GN⊥AC；
（Ⅱ）求三棱锥F-MCE的体积；
（Ⅲ）当FG=GD时，证明AG∥平面FMC．

Answer 1

分析：（Ⅰ）由三视图易得该几何体是一个底面为等腰直角三角形的直三棱柱，且侧面积ABCD是正方形，根据已知，我们易得AC⊥面ABCD
，进而得到GN⊥AC．
（Ⅱ）利用转化思想，我们可得V_E-FMC=V_ADF-BCE-V_F-AMCD-V_E-MBC，把相应的棱长代入体积公式，即可得到结论．
（Ⅲ）连接DE交FC于Q，连接QG，我们易得AM∥GQ，根据线面平行的判定定理，我们易得结论．

解答：解：（Ⅰ）由三视图可知，多面体是直三棱柱，
两底面是直角边长为a的等腰直角三角形，
侧面ABCD，CDFE是边长为a的正方形．（3分）
连接DN，因为FD⊥CD，FD⊥AD，
所以，FD⊥面ABCD
∴FD⊥AC
又∵AC⊥DN，
所以，AC⊥面GND，
GN?面GND
所以GN⊥AC（6分）
（Ⅱ）V_E-FMC=V_ADF-BCE-V_F-AMCD-V_E-MBC．（12分）
=S△BCE•CD-

1

3

FD•SAMCD-

1

3

EC•S△MBC
=

1

2

a•a•a-

1

3

•

1

2

(

a

2

+a)•a•a-

1

3

•

1

2

•

a

2

•a•a
=

1

6

a3．（14分）
另解：VE-FMC=VM-CEF=

1

3

AD•S△CEF=

1

3

•a•

1

2

a•a=

1

6

a3
（Ⅲ）连接DE交FC于Q，连接QG
因为G，Q，M分别是FD，FC，AB的中点，所以GQ∥

1

2

CD，AM∥

1

2

CD，
所以，AM∥GQ，AMGQ是平行四边形（9分）
AG∥QM，AG?面FMC，MQ?面FMC
所以，AG∥平面FMC．（10分）

点评：本题考查的知识点是由三视图判断物体的形状，线面、线线垂直的转化，棱锥体积的求法，线面平行的证明，其中根据三视图判断棱柱相关棱长的长度及相互之间的关系是解答本题的关键．