Question

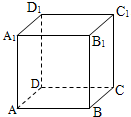如图，在正方体ABCD-A₁B₁C₁D₁的侧面AB₁内有一动点P到A₁B₁与BC的距离之比为定值，则动点P所在的曲线可能为（　　）

A．

B．

C．

D．

Answer 1

分析：点P到BC的距离可以转化为P到点B的距离，故动点P到A₁B₁与点B的距离之比为定值，所以点P所在曲线以点B为焦点，以A₁B₁为准线的椭圆（或双曲线、或抛物线）的一部分．

解答：解：∵在正方体ABCD-A₁B₁C₁D₁的侧面AB₁内有一动点P到A₁B₁与BC的距离之比为定值，
BC⊥平面ABB₁A₁，
∴点P到BC的距离可以转化为P到点B的距离，
∴动点P到A₁B₁与点B的距离之比为定值，
符合圆锥曲线的第二定义的要求，
所以点P所在曲线以点B为焦点，以A₁B₁为准线的椭圆（或双曲线、或抛物线）的一部分，
故选D．

点评：本题考查圆锥曲线的第二定义的应用，解题时要认真审题，仔细解答，注意合理地进行等价转化．