Question

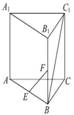
如图所示．三棱柱A_。B_。C₁―ABC的侧面BCC₁B₁是菱形，∠CBB₁=60°，AB⊥面BCC_lB₁，AB=3，BB₁=4．

(1)求证：B_lC⊥AC₁；

(2)若D是AB的中点，求二面角D―CC₁―B的平面角的余弦值．

Answer 1

解：(1)证明：连接BC₁，∵侧面BCC₁B₁是菱形，

    ∴BC_l⊥B₁C，

又∵AB⊥面BCC₁B₁，∴AB⊥BC₁，BC₁是AC₁在面BCC₁B₁内的射影，

由三垂线定理得B₁C⊥AC₁

    (2)取A_lB₁的中点D₁，连接DD_l、D₁C、D₁C₁，过D₁作D₁E⊥CC₁于E，连接B₁E，

    ∵AB⊥面BCC_lB₁，

    ∴A₁B₁⊥面BCC₁B₁，即D₁B₁⊥面BCC₁B₁，

    ∴∠D_IEB₁为二面角D―CC₁―B的平而角

    ∵BCC₁B₁为菱形，∴CC₁=BB₁=4，又

    ∵∠CBB₁=60°，∴△B₁CC₁为等边三角形

    ∴B₁E=2，由D_lB₁=得 D₁E=

    ∴cos∠D_l EB₁=

    即二面角D―CC₁―B的平面角的余弦值为