题目内容
【题目】由团中央学校部、全国学联秘书处、中国青年报社共同举办的2018年度全国“最美中学生”寻访活动结果出炉啦，此项活动于2018年6月启动，面向全国中学在校学生，通过投票方式寻访一批在热爱祖国、勤奋学习、热心助人、见义勇为等方面表现突出、自觉树立和践行社会主义核心价值观的“最美中学生”.现随机抽取了30名学生的票数，绘成如图所示的茎叶图，若规定票数在65票以上（包括65票）定义为风华组.票数在65票以下（不包括65票）的学生定义为青春组.
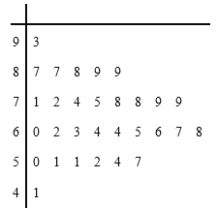
（1）如果用分层抽样的方法从青春组和风华组中抽取5人，再从这5人中随机抽取2人，那么至少有1人在青春组的概率是多少？
（2）用样本估计总体，把频率作为概率，若从该地区所有的中学（人数很多）中随机选取4人，用
表示所选4人中青春组的人数，试写出的分布列，并求出的数学期望.
【答案】（1）
；（2）分布列见解析，
【解析】
（1） 用A表示“至少有1人在青春组”，利用对立事件概率计算公式能求出至少有1人在青春组的概率.
（2）由题知，抽取的30名学生中有12名学生是青春组学生，抽取1名学生是青春组学生的概率为
，从所有的中学生中抽取1名学生是甲组学生的概率是
，
服从二项分布
.由此能求出的分布列、数学期望.
解：（1） 用A表示“至少有1人在青春组”，
则至少有1人在青春组的概率为
；
（2）由题知，抽取的30名学生中有12名学生是青春组学生，抽取1名学生是青春组学生的概率为，
那么从所有的中学生中抽取1名学生是甲组学生的概率是，
又因为所取总体数量较多，抽取4名学生可以看出4次独立重复实验，于是服从二项分布.的取值为0，1，2，3，4.且
.
所以得的分布列为：
|
|
|
|
|
|
|
|
|
|
|
|
数学期望
.
【题目】某校高三（1）班在一次语文测试结束后，发现同学们在背诵内容方面失分较为严重.为了提升背诵效果，班主任倡议大家在早晩读时间站起来大声诵读，为了解同学们对站起来大声诵读的态度，对全班50名同学进行调查，将调查结果进行整理后制成如表：
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
（1）欲使测试优秀率为
，则优秀分数线应定为多少分？
（2）依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系，列出2×2列联表，并判断是否有
的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据：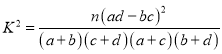
，
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
