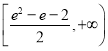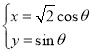题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为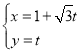 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]()
(1)求圆![]() 的圆心到直线
的圆心到直线![]() 的距离;
的距离;
(2)己知![]() ,若直线
,若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)将直线![]() 的参数方程转化为普通方程,将圆
的参数方程转化为普通方程,将圆![]() 的极坐标方程转化为直角坐标方程,并求得圆心坐标,利用点到直线的距离公式求得圆
的极坐标方程转化为直角坐标方程,并求得圆心坐标,利用点到直线的距离公式求得圆![]() 圆心到直线
圆心到直线![]() 的距离.
的距离.
(2)设出直线![]() 的参数方程,代入圆的方程,写出韦达定理,根据直线参数方程参数的几何意义,求得
的参数方程,代入圆的方程,写出韦达定理,根据直线参数方程参数的几何意义,求得![]() 的值.
的值.
(1)由直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),消去参数
为参数),消去参数![]() ,可得
,可得![]() .
.
圆![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() ,
,
∴圆![]() 的普通坐标方程为
的普通坐标方程为![]() ,则圆心
,则圆心![]()
∴圆心![]() ,到直线
,到直线![]() 的距离
的距离![]()
(2)已知![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与圆
与圆![]() 交于
交于![]() 两点,将
两点,将 (
(![]() 为参数)代入圆
为参数)代入圆![]() 的普通坐标方程
的普通坐标方程![]() ,得
,得![]()
设![]() ,
,![]() 对应参数为
对应参数为![]() ,
,![]() ,则
,则![]() ,
,![]()
∵![]() ,
,![]() ,∴
,∴![]() 是同为负号.
是同为负号.
∴ .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某理财公司有两种理财产品![]() 和
和![]() ,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]()
投资结果 | 获利20% | 获利10% | 不赔不赚 | 亏损10% |
概率 | 0.2 | 0.3 | 0.2 | 0.3 |
产品![]() (其中
(其中![]() )
)
投资结果 | 获利30% | 不赔不赚 | 亏损20% |
概率 |
| 0.1 |
|
(1)已知甲、乙两人分别选择了产品![]() 和产品
和产品![]() 进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求
进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求![]() 的取值范围;
的取值范围;
(2)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品![]() 和产品
和产品![]() 之中选其一,应选用哪种产品?
之中选其一,应选用哪种产品?