题目内容
若直线L倾斜角的余弦值为
,则直线L的斜率为( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、±
| ||
D、±
|
分析:根据倾斜角的余弦值,由倾斜角的范围,利用同角三角函数间的基本关系求出倾斜角的正弦函数值,然后求出倾斜角的正切值即为此直线的斜率.
解答:解:由 cosα=
(0≤α<π),
得 sinα=
.
所以 k=tanα=
=
.
故选B.
| 3 |
| 5 |
得 sinα=
| 4 |
| 5 |
所以 k=tanα=
| sinα |
| cosα |
| 4 |
| 3 |
故选B.
点评:此题考查学生掌握倾斜角的三角函数值与直线的斜率的关系,解题过程中要注意倾斜角的范围,是一道基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 ,则直线L的斜率为
,则直线L的斜率为

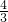
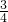
 ,则直线L的斜率为( )
,则直线L的斜率为( )


