题目内容
一个所有棱长均为1的正四棱锥的顶点与底面的四个顶点均在某个球的球面上，则此球的体积为（ ）
A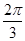． | B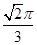． | C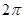． | D． |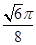
B
解析试题分析：
设四棱锥
是满足条件的，连结
、
交于
，球心
在
上，
令球的半径为
，则
，
由正四棱锥所有棱长为1，易求得四棱锥的高
，
在
中，
，即
，解得
，
故球的体积为
. 选B.
考点：正四棱锥的性质，球的体积.
练习册系列答案
相关题目
将棱长为2的正方体木块削成一个体积最大的球，则这个球的表面积为（ ）
A．2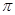 | B．4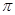 | C．8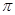 | D．16 |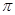
某几何体的三视图及部分数据如图所示，则此几何体的体积是( ) 
A． | B． | C． | D． |
某几何体的三视图如图所示，则它的侧面积为（ ）
A． | B． | C．24 | D． |
某几何体的三视图如图所示，则它的体积是（ ）
A． | B． | C． | D． |
一个正四棱锥的正(主)视图如右图所示，该四棱锥侧面积和体积分别是（ ）
A． ， | B．， |
C． ， | D．， |
的底面面积为
，体积为
，
为侧棱
的中点，则
与
所成的角为 （ ）
的圆，则这个几何体的体积是（ ）
