题目内容
已知![]() ,且
,且![]()
1.设![]() ,求
,求![]() 的解析式;
的解析式;
2.设![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使
,使![]() 在
在![]() 内为减函数,且在(-1,0)内是增函数.
内为减函数,且在(-1,0)内是增函数.
1.由题意得![]() ,
,
![]() ,
,
∴![]()
∴![]()
2.![]() .
.
若满足条件的![]() 存在,则
存在,则![]()
∵函数![]() 在
在![]() 内是减函数,∴当
内是减函数,∴当![]() 时,
时,![]() ,
,
即![]() 对于
对于![]() 恒成立.
恒成立.
∴![]()
∴![]() ,解得
,解得![]() .
.
又函数![]() 在(-1,0)上是增函数,∴当
在(-1,0)上是增函数,∴当![]() 时,
时,![]()
即![]() 对于
对于![]() 恒成立,
恒成立,
∴![]()
∴![]() ,解得
,解得![]() .
.
故当![]() 时,
时,![]() 在
在![]() 上是减函数,在(-1,0)上是增函数,即满足条件的
上是减函数,在(-1,0)上是增函数,即满足条件的![]() 存在.
存在.
解析:
根据题设条件可以求出![]() 的表达式,对于探索性问题,一般先对结论做肯定存在的假设,然后由此肯定的假设出发,结合已知条件进行推理论证,由推证结果是否出现矛盾来作出判断.解题的过程实质是一种转化的过程,由于函数
的表达式,对于探索性问题,一般先对结论做肯定存在的假设,然后由此肯定的假设出发,结合已知条件进行推理论证,由推证结果是否出现矛盾来作出判断.解题的过程实质是一种转化的过程,由于函数![]() 是可导函数,因此选择好解题的突破口,要充分利用函数的单调性构造等价的不等式,确定适合条件的参数
是可导函数,因此选择好解题的突破口,要充分利用函数的单调性构造等价的不等式,确定适合条件的参数![]() 的取值范围,使问题获解.
的取值范围,使问题获解.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 .
. ,求函数
,求函数 的极值;
的极值; ,且当
,且当 时,
时,
 12a恒成立,试确定
12a恒成立,试确定 的取值范围.
的取值范围.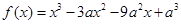 .
.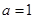 ,求函数
,求函数 的极值;
的极值; ,且当
,且当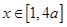 时,
时,
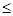 12a恒成立,试确定
12a恒成立,试确定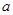 的取值范围.
的取值范围. .
. ,求函数
,求函数 的极值;
的极值; ,且当
,且当 时,
时,
 12a恒成立,试确定
12a恒成立,试确定 的取值范围
的取值范围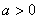 ,且
,且 ≠1,设
≠1,设 函数
函数 在
在 内单调递减;q:函数
内单调递减;q:函数 有两个不同零点点,如果
有两个不同零点点,如果 和
和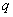 有且只有一个正确,求
有且只有一个正确,求