题目内容
(14分)已知动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半,
求:(1)动点M的轨迹方程;(2)若N为线段AM的中点,试求点N的轨迹.
【答案】
(1)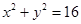 (2)
(2)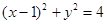 ,N的轨迹是以(1,0)为圆心,以2为半径的圆.
,N的轨迹是以(1,0)为圆心,以2为半径的圆.
【解析】
试题分析:解:(1)设动点M(x,y)为轨迹上任意一点,则点M的轨迹就是集合
P 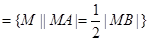 .
.
由两点距离公式,点M适合的条件可表示为  ,
,
平方后再整理,得
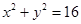 . 可以验证,这就是动点M的轨迹方程.
. 可以验证,这就是动点M的轨迹方程.
(2)设动点N的坐标为(x,y),M的坐标是(x1,y1).
由于A(2,0),且N为线段AM的中点,所以
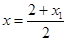 ,
, 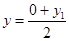 .所以有
.所以有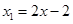 ,
,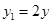 ①
①
由(1)题知,M是圆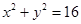 上的点,
上的点,
所以M坐标(x1,y1)满足: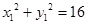 ②
②
将①代入②整理,得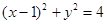 .
.
所以N的轨迹是以(1,0)为圆心,以2为半径的圆.
考点:本题主要考查求轨迹方程的基本方法—-直接法和相关点法,考查考生的计算能力。
点评:求轨迹方程的基本方法—-直接法和相关点法,应熟练掌握。两道小题有相互对比之效。

练习册系列答案
相关题目
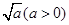 倍,求:(1)动点M的轨迹方程;(2)根据
倍,求:(1)动点M的轨迹方程;(2)根据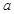 取值范围指出轨迹表示的图形.
取值范围指出轨迹表示的图形.