题目内容
在等比数列{an}中,an>0(n∈N*),公比q∈(0,1),且a3+a5=5,又a3与a5的等比中项为2.
(1)求数列{an}的通项公式;
(2)设bn=5-log2an,数列{bn}的前n项和为Sn,求数列{Sn}的通项公式;
(3)设Tn=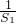 +
+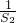 +…+
+…+ ,求Tn.
,求Tn.
解:(1)an>0,∴a3+a5=5,又a3与a5的等比中项为2,∴a3a5=4,而q∈(0,1),
∴a3>a5,∴a3=4,a5=1,∴q= ,a1=16,
,a1=16,
∴an=16× =25-n;
=25-n;
(2)bn=5-log2an=5-(5-n)=n,∴bn+1-bn=1,
∴{bn}是以b1=1为首项,1为公差的等差数列.
∴Sn= ;
;
(3)由(2)知 =
=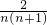 =2(
=2( -
- )
)
∴Tn=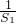 +
+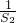 ++
++ =2[(1-
=2[(1- )+(
)+( -
- )++(
)++( -
- )=2(1-
)=2(1- )=
)= ;
;
分析:(1)直接利用a3+a5=5,以及a3与a5的等比中项为2即可求出a3和a5,进而求出数列{an}的通项公式;
(2)先把(1)的结论代入整理出数列{bn}的通项公式,得数列{bn}为等差数列,再代入等差数列的求和公式即可;
(3)先利用(2)的结论知 =
=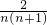 =2(
=2( -
- ),再代入求和即可.
),再代入求和即可.
点评:本题考查等差数列与等比数列的基础知识以及数列求和的裂项法,是对基础知识的考查,属于中档题.
∴a3>a5,∴a3=4,a5=1,∴q=
 ,a1=16,
,a1=16,∴an=16×
 =25-n;
=25-n;(2)bn=5-log2an=5-(5-n)=n,∴bn+1-bn=1,
∴{bn}是以b1=1为首项,1为公差的等差数列.
∴Sn=
 ;
;(3)由(2)知
 =
=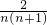 =2(
=2( -
- )
)∴Tn=
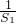 +
+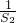 ++
++ =2[(1-
=2[(1- )+(
)+( -
- )++(
)++( -
- )=2(1-
)=2(1- )=
)= ;
;分析:(1)直接利用a3+a5=5,以及a3与a5的等比中项为2即可求出a3和a5,进而求出数列{an}的通项公式;
(2)先把(1)的结论代入整理出数列{bn}的通项公式,得数列{bn}为等差数列,再代入等差数列的求和公式即可;
(3)先利用(2)的结论知
 =
=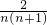 =2(
=2( -
- ),再代入求和即可.
),再代入求和即可.点评:本题考查等差数列与等比数列的基础知识以及数列求和的裂项法,是对基础知识的考查,属于中档题.

练习册系列答案
相关题目
在等比数列{an}中,若a1=1,公比q=2,则a12+a22+…+an2=( )
| A、(2n-1)2 | ||
B、
| ||
| C、4n-1 | ||
D、
|