题目内容
下列四个函数，在x=0处取得极值的函数是（ ）
①y=x3 ②y=x2+1 ③y=|x| ④y=2x
| A．①② | B．②③ | C．③④ | D．①③ |
B
解析试题分析：根据函数极值的定义，①
,在
处无极值；④
，在处无极值．
考点：函数的极值．
练习册系列答案
相关题目
函数
在区间
上单调递增，则实数
的取值范围是（ ）
A． | B． | C． | D． |
若
，其中
，则
( )
A． | B． | C． | D． |
已知函数f(x)＝
x4－2x3＋3m，x∈R，若f(x)＋9≥0恒成立，则实数m的取值范围是( )
A．m≥ | B．m> | C．m≤ | D．m< |
如图，抛物线
与直线
围成的封闭区域为M，则区域M的面积为（ ）
| A．6 | B． | C． | D．8 |
已知函数f(x)(x∈R)满足f(1)＝1，且f(x)的导函数f′(x)<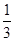
，则f(x)<
＋
的解集为( )
| A．{x|－1<x<1} | B．{x|x<－1} |
| C．{x|x<－1或x>1} | D．{x|x>1} |
[2014·山东济宁]已知f(x)＝
x2＋2xf′(2014)＋2014lnx，则f′(2014)＝( )
| A．2015 | B．－2015 | C．2014 | D．－2014 |
（2011•湖北）放射性元素由于不断有原子放射出微粒子而变成其他元素，其含量不断减少，这种现象称为衰变．假设在放射性同位素铯137的衰变过程中，其含量M（单位：太贝克）与时间t（单位：年）满足函数关系：M（t）=M0
，其中M0为t=0时铯137的含量．已知t=30时，铯137含量的变化率是﹣10In2（太贝克/年），则M（60）=（ ）
| A．5太贝克 | B．75In2太贝克 | C．150In2太贝克 | D．150太贝克 |
已知定义在R上的函数f(x)，其导函数f′(x)的大致图象如图所示，则下列叙述正确的是( )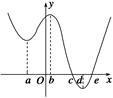
| A．f(b)>f(c)>f(d) |
| B．f(b)>f(a)>f(e) |
| C．f(c)>f(b)>f(a) |
| D．f(c)>f(e)>f(d) |