题目内容
设圆锥的母线长为l,底面半径为r,满足条件“它的一个内接圆柱的侧面积等于圆锥侧面积的 ”的情况有且只有一种,则
”的情况有且只有一种,则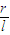 = .
= .
【答案】分析:由题意画出圆锥及其内接圆柱的轴截面图,设出圆锥的高,圆柱的高和底面半径,然后根据平行关系建立方程,由满足条件“圆锥的一个内接圆柱的侧面积等于圆锥侧面积的 ”的情况有且只有一种知方程有唯一解,利用方程的判别式等于0得圆锥的母线长l与底面半径r的关系.
”的情况有且只有一种知方程有唯一解,利用方程的判别式等于0得圆锥的母线长l与底面半径r的关系.
解答: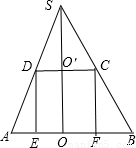 解:由题意画出轴截面图,如图所示,
解:由题意画出轴截面图,如图所示,
圆锥的母线长为l,底面半径为r,
设圆锥高为h,内接圆柱高为x,底面半径为y,
∵CD∥AB,∴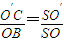 ,∴
,∴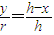 ,则
,则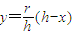 ,
,
∴圆锥的侧面积S1=πrl,圆柱的侧面积S2=2πx•y=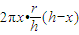 .
.
由圆锥的一个内接圆柱的侧面积等于圆锥侧面积的 得:
得: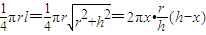 ,
,
即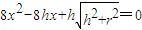 ,也就是
,也就是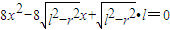 .
.
又“圆锥的一个内接圆柱的侧面积等于圆锥侧面积的 ”的情况有且只有一种
”的情况有且只有一种
∴方程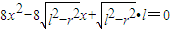 有且只有一个解,
有且只有一个解,
∴△=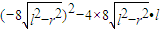 =0,
=0,
即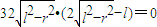 .
.
∵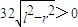 ,
,
∴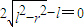 ,
,
整理得: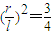 ,∴
,∴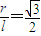 .
.
∴圆锥的母线长为l,底面半径为r,满足条件“它的一个内接圆柱的侧面积等于圆锥侧面积的 ”的情况有且只有一种时的
”的情况有且只有一种时的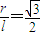 .
.
故答案为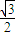 .
.
点评:本题考查了旋转体中组合体的关系,考查了学生的观察与分析能力,考查了空间想象能力,解答此题的关键是把题目给出的条件转化成方程有唯一解,体现了数学转化思想,同时训练了学生对一元二次方程有唯一解情况的处理,是中档题.
 ”的情况有且只有一种知方程有唯一解,利用方程的判别式等于0得圆锥的母线长l与底面半径r的关系.
”的情况有且只有一种知方程有唯一解,利用方程的判别式等于0得圆锥的母线长l与底面半径r的关系.解答:
 解:由题意画出轴截面图,如图所示,
解:由题意画出轴截面图,如图所示,圆锥的母线长为l,底面半径为r,
设圆锥高为h,内接圆柱高为x,底面半径为y,
∵CD∥AB,∴
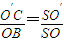 ,∴
,∴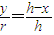 ,则
,则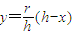 ,
,∴圆锥的侧面积S1=πrl,圆柱的侧面积S2=2πx•y=
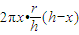 .
.由圆锥的一个内接圆柱的侧面积等于圆锥侧面积的
 得:
得: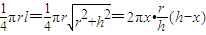 ,
,即
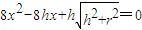 ,也就是
,也就是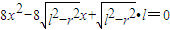 .
.又“圆锥的一个内接圆柱的侧面积等于圆锥侧面积的
 ”的情况有且只有一种
”的情况有且只有一种∴方程
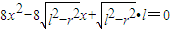 有且只有一个解,
有且只有一个解,∴△=
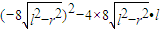 =0,
=0,即
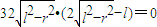 .
.∵
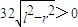 ,
,∴
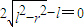 ,
,整理得:
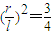 ,∴
,∴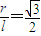 .
.∴圆锥的母线长为l,底面半径为r,满足条件“它的一个内接圆柱的侧面积等于圆锥侧面积的
 ”的情况有且只有一种时的
”的情况有且只有一种时的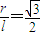 .
.故答案为
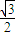 .
.点评:本题考查了旋转体中组合体的关系,考查了学生的观察与分析能力,考查了空间想象能力,解答此题的关键是把题目给出的条件转化成方程有唯一解,体现了数学转化思想,同时训练了学生对一元二次方程有唯一解情况的处理,是中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目

 ”的情况有且只有一种,则
”的情况有且只有一种,则 =________.
=________.