题目内容
一排有七个车位,A、B两辆汽车停在其中的两个车位上,要求A与B之间至少有一个空车位,则不同的停车方式有
- A.16种
- B.28种
- C.30种
- D.42种
C
分析:方法一:利用“捆绑法”、“插空法”即可得出.
方法二:利用间接法,先求出没有要求的放法,再求出AB汽车相邻的放法,减去即可得到.
解答:方法一:①若汽车A与B之间有一个空车位,可有 =10种方法;
=10种方法;
②若汽车A与B之间有两个空车位,可有 =8种方法;
=8种方法;
③若汽车A与B之间有3个空车位,可有 =6种方法;
=6种方法;
④若汽车A与B之间有4个空车位,可有 =4种方法;
=4种方法;
⑤若汽车A与B之间有5个空车位,可有 =2种方法.
=2种方法.
综上可知:共有10+8+6+4+2=30种方法.
方法二:若A、B两辆汽车停在7七个车位的其中的两个车位上,则有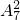 =42种放法,其中AB汽车相邻的方法有
=42种放法,其中AB汽车相邻的方法有 =12种方法,因此要求A与B之间至少有一个空车位的不同的停车方式有42-12=30种方法.
=12种方法,因此要求A与B之间至少有一个空车位的不同的停车方式有42-12=30种方法.
故选C.
点评:熟练掌握“捆绑法”、“插空法”、“间接法”及排列与组合的计算公式是解题的关键.
分析:方法一:利用“捆绑法”、“插空法”即可得出.
方法二:利用间接法,先求出没有要求的放法,再求出AB汽车相邻的放法,减去即可得到.
解答:方法一:①若汽车A与B之间有一个空车位,可有
 =10种方法;
=10种方法;②若汽车A与B之间有两个空车位,可有
 =8种方法;
=8种方法;③若汽车A与B之间有3个空车位,可有
 =6种方法;
=6种方法;④若汽车A与B之间有4个空车位,可有
 =4种方法;
=4种方法;⑤若汽车A与B之间有5个空车位,可有
 =2种方法.
=2种方法.综上可知:共有10+8+6+4+2=30种方法.
方法二:若A、B两辆汽车停在7七个车位的其中的两个车位上,则有
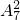 =42种放法,其中AB汽车相邻的方法有
=42种放法,其中AB汽车相邻的方法有 =12种方法,因此要求A与B之间至少有一个空车位的不同的停车方式有42-12=30种方法.
=12种方法,因此要求A与B之间至少有一个空车位的不同的停车方式有42-12=30种方法.故选C.
点评:熟练掌握“捆绑法”、“插空法”、“间接法”及排列与组合的计算公式是解题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目