题目内容
在直角坐标系xOy中，设P为两动圆（x+2）2+y2=（r+2）2，（x-2）2+y2=r2（r＞1）的一个交点，记动点P的轨迹为C．给出下列三个结论：①曲线C过坐标原点；
②曲线C关于x轴对称；
③设点P（x，y），则有|y|＜|2x|．
其中，所有正确的结论序号是 ．
【答案】分析：根据P到两圆圆心的距离之差是定值，根据双曲线定义判断曲线类型，再写出方程；然后利用方程验证是否过原点，是否关于x轴对称，是否满足|y|＜|2x|即可．
解答：解：设A（-2，0），B（2，0），动点P（x，y），
根据题意：|PA|-|PB|=2
∴根据双曲线的定义判定，P点的轨迹是双曲线的右支，
方程式：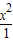
-
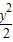=1，（x＞0）
∵（0，0）不是方程的解，∴①不正确；
设点M（x，y）曲线上的任一点，M关于x轴的对称点为N（x，-y），
∵N的坐标也满足方程，∴N在曲线上，∴曲线C关于x轴对称，②正确；
∵4x2=4（1+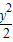
）=4+2y2＞y2，∴|y|＜|2x|．故③正确．
答案是②③
点评：本题借助考查命题的真假判断，考查双曲线的定义及定义法求轨迹方程．
定义法求轨迹方程的基本步骤：根据条件判断动点轨迹类型--根据已知曲线的标准方程求出特征量--写出轨迹方程，再证明以方程的解为坐标的点都在曲线上．
解答：解：设A（-2，0），B（2，0），动点P（x，y），
根据题意：|PA|-|PB|=2
∴根据双曲线的定义判定，P点的轨迹是双曲线的右支，
方程式：
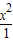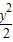-=1，（x＞0）∵（0，0）不是方程的解，∴①不正确；
设点M（x，y）曲线上的任一点，M关于x轴的对称点为N（x，-y），
∵N的坐标也满足方程，∴N在曲线上，∴曲线C关于x轴对称，②正确；
∵4x2=4（1+
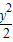）=4+2y2＞y2，∴|y|＜|2x|．故③正确．答案是②③
点评：本题借助考查命题的真假判断，考查双曲线的定义及定义法求轨迹方程．
定义法求轨迹方程的基本步骤：根据条件判断动点轨迹类型--根据已知曲线的标准方程求出特征量--写出轨迹方程，再证明以方程的解为坐标的点都在曲线上．
练习册系列答案
相关题目
如图所示，在直角坐标系xOy中，射线OA在第一象限，且与x轴的正半轴成定角60°，动点P在射线OA上运动，动点Q在y轴的正半轴上运动，△POQ的面积为