题目内容
已知函数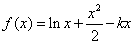 ,其中常数
,其中常数 .
.
(1) 求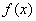 的单调增区间与单调减区间;
的单调增区间与单调减区间;
(2)若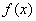 存在极值且有唯一零点
存在极值且有唯一零点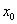 ,求
,求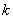 的取值范围及不超过
的取值范围及不超过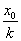 的最大整数
的最大整数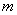 .
.
请考生在第22、23、24三题中任选一题做答,如果多做。则按所做的第一题记分.答题时用2B铅笔在答题卡上把所选的题号涂黑.
解:(1)
① 当 时,
时, ,函数
,函数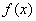 为增函数.、
为增函数.、
②当 时,
时, ,其中
,其中
 的取值变化情况如下表:
的取值变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
综合①②知当 时,
时,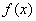 的增区间为
的增区间为 ,无减区间;
,无减区间;
当 时,
时,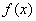 的增区间为
的增区间为 与
与 ,
,
减区间为
(2)由(1)知当 时,
时,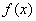 无极值;
无极值;
当 时,
时, 知
知
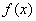 的极大值
的极大值 ,
,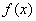 的极小值
的极小值 ,
,
故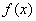 在
在 上无零点.
上无零点.
 ,又
,又 ,
,
故函数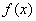 有唯一零点
有唯一零点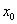 ,且
,且
又 ,记
,记 ,
,
 则
则 ,
,
从而 ,
,
故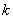 的取值范围是
的取值范围是 不超过
不超过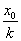 的最大整数
的最大整数

练习册系列答案
相关题目









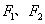 为椭圆
为椭圆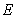 的左右焦点,点
的左右焦点,点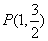 为其上一点,且有
为其上一点,且有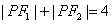
 的标准方程;
的标准方程;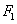 的直线
的直线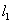 与椭圆
与椭圆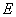 交于
交于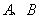 两点,过
两点,过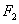 与
与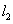 与椭圆
与椭圆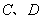 两点,求四边形
两点,求四边形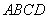 的面积
的面积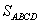 的最大值.
的最大值. 分别是正方体
分别是正方体 的棱
的棱 的中点,点
的中点,点 分别是线段
分别是线段 与
与 上的点,则与平面
上的点,则与平面 垂直的直线
垂直的直线 有 条。
有 条。
 B.
B.
 D.
D.

 与曲线
与曲线 相交于点
相交于点 ,且曲线
,且曲线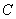 在
在 的值为________.
的值为________. 在定义域R内连续可导,若
在定义域R内连续可导,若 ,且当
,且当 时,
时, ,设
,设 则( )
则( ) B.
B. C.
C. D.
D.
 (
( )的图象上有一点
)的图象上有一点 ,该函数的图象与 x轴、直线x=-1及 x=t围成图形(如图阴影部分)的面积为S,则S与t的函数关系图可表示为( )
,该函数的图象与 x轴、直线x=-1及 x=t围成图形(如图阴影部分)的面积为S,则S与t的函数关系图可表示为( )
 (x2+2x)
(x2+2x) D.y=0.2+log16x
D.y=0.2+log16x