[题目]已知.命题方程表示焦点在轴上的椭圆.命题方程表示双曲线.(1)若命题是真命题.求实数的范围,(2)若命题“或为真命题.“且是假命题.求实数的范围. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知，命题方程表示焦点在轴上的椭圆，命题方程表示双曲线.

（1）若命题是真命题，求实数的范围；

（2）若命题“或”为真命题，“且”是假命题，求实数的范围.

【答案】（1）；（2）.

【解析】

由方程表示焦点在y轴上的椭圆，根据椭圆的几何性质可得，，求解不等式可得答案；由双曲线的几何性质求出为真命题的的范围，结合，由为真命题，为假命题，可得一真一假，分两种情况讨论，对于真假以及假真分别列不等式组，分别解不等式组，然后求并集即可求得实数的取值范围.

若命题p是真命题，则，解得；

若命题q为真命题，则，即．

命题“p或q”为真命题，“p且q”为假命题，则p，q一真一假．

当p真q假时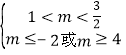，，得；

当p假q真时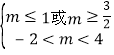，，解得或．

实数m的取值范围时．

练习册系列答案

相关题目

【题目】已知直线l：y=k（x+2）与圆O：x2+y2=4相交于不重合的A、B两点，O是坐标原点，且三点A、B、O构成三角形．

（1）求k的取值范围；

（2）三角形ABO的面积为S，试将S表示成k的函数，并求出它的定义域；

（3）求S的最大值，并求取得最大值时k的值．

【题目】设抛物线x2=4y的焦点为F，过点F作斜率为k（k＞0）的直线l与抛物线相交于A、B两点，且点P恰为AB的中点，过点P作x轴的垂线与抛物线交于点M，若|MF|=4，则直线l的方程为（）
A.
B.y= x+1
C.
D.

【题目】已知，，则下列结论中正确的是（）
A.函数y=f（x）?g（x）的周期为2
B.函数y=f（x）?g（x）的最大值为1
C.将f（x）的图象向左平移个单位后得到g（x）的图象
D.将f（x）的图象向右平移个单位后得到g（x）的图象

【题目】雾霾大气严重影响人们的生活，某科技公司拟投资开发新型节能环保产品，策划部制定投资计划时，不仅要考虑可能获得的盈利，而且还要考虑可能出现的亏损，经过市场调查，公司打算投资甲、乙两个项目，根据预测，甲、乙项目可能的最大盈利率分别为和，可能的最大亏损率分别为和，投资人计划投资金额不超过9万元，要求确保可能的资金亏损不超过万元．

Ⅰ若投资人用x万元投资甲项目，y万元投资乙项目，试写出x，y所满足的条件，并在直角坐标系内作出表示x，y范围的图形．

Ⅱ根据的规划，投资公司对甲、乙两个项目分别投资多少万元，才能使可能的盈利最大？

【题目】已知，．

当时，求函数图象过的定点；

当，，且有最小值2时，求a的值；

当，时，有恒成立，求实数t的取值范围．

【题目】设函数f（x）=lnx，g（x）= （m＞0）．
（1）当m=1时，函数y=f（x）与y=g（x）在x=1处的切线互相垂直，求n的值；
（2）若对任意x＞0，恒有|f（x）|≥|g（x）|成立，求实数n的值及实数m的最大值．

【题目】已知三棱台ABC﹣A1B1C1中，平面BB1C1C⊥平面ABC，∠ACB=90°，BB1=CC1=B1C1=2，BC=4，AC=6
（1）求证：BC1⊥平面AA1C1C
（2）点D是B1C1的中点，求二面角A1﹣BD﹣B1的余弦值．

【题目】定义在区间D上的函数f（x）和g（x），如果对任意x∈D，都有|f（x）﹣g（x）|≤1成立，则称f（x）在区间D上可被g（x）替代，D称为“替代区间”．给出以下问题：
①f（x）=x2+1在区间（﹣∞，+∞）上可被g（x）=x2+ 替代；
②如果f（x）=lnx在区间[1，e]可被g（x）=x﹣b替代，则﹣2≤b≤2；
③设f（x）=lg（ax2+x）（x∈D1），g（x）=sinx（x∈D1），则存在实数a（a≠0）及区间D1 ， D2 ，使得f（x）在区间D1∩D2上被g（x）替代．
其中真命题是（）
A.①②③
B.②③
C.①
D.①②

试题分类