Question

【题目】设和是两个等差数列，记 ，

其中表示这个数中最大的数．

（Ⅰ）若， ，求的值，并证明是等差数列；

（Ⅱ）证明：或者对任意正数，存在正整数，当时， ；或者存在正整数，使得是等差数列．

Answer 1

【答案】（1）见解析（2）见解析

【解析】试题分析：（Ⅰ）分别代入求，观察规律，再证明当时， ，所以关于单调递减. 所以，从而得证；（Ⅱ）首先求的通项公式，分三种情况讨论证明.

试题解析：（Ⅰ）

，

.

当时， ，

所以关于单调递减.

所以.

所以对任意，于是，

所以是等差数列.

（Ⅱ）设数列和的公差分别为，则

.

所以

①当时，取正整数，则当时， ，因此.

此时， 是等差数列.

②当时，对任意，

此时， 是等差数列.

③当时，

当时，有.

所以

对任意正数，取正整数，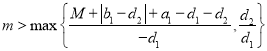

故当时， .