题目内容
(本小题满分13分)如图,三棱柱 中,
中, ,
, ,
, .
.

(1)证明: ;
;
(2)若 ,
, ,求二面角
,求二面角 的余弦值.
的余弦值.
(1)证明详见解析;(2) .
.
【解析】
试题分析:本题主要以三棱柱为几何背景考查线线垂直、线面垂直、二面角等基础知识,考查学生的分析问题解决问题的能力、空间想象能力、逻辑推理能力、计算能力.第一问,在等腰三角形中,O为AB中点,所以CO为高,由已知可得 为等边三角形,所以得到
为等边三角形,所以得到 ,所以利用线面垂直的判定得
,所以利用线面垂直的判定得 平面
平面 ,最后利用线面垂直的性质得
,最后利用线面垂直的性质得 ;第二问,在等边三角形中,先解出边CO和
;第二问,在等边三角形中,先解出边CO和 的长,再利用
的长,再利用 分析出
分析出 是直角三角形,得到线段的两两垂直关系,从而建立空间直角坐标系,得到平面
是直角三角形,得到线段的两两垂直关系,从而建立空间直角坐标系,得到平面 和平面ACB的法向量,再利用夹角公式计算二面角的余弦值.
和平面ACB的法向量,再利用夹角公式计算二面角的余弦值.
试题解析:(1)证明:取 的中点
的中点 ,连接
,连接 ,
, ,
, .
.

 ,故
,故 , . ..1分
, . ..1分
又 ,
, ,
,
 为等边三角形.
为等边三角形.
 , ..3分
, ..3分
又因为 平面
平面 ,
, 平面
平面 ,
, .
.
 平面
平面 . 5分
. 5分
又 平面
平面 ,因此
,因此 . 6分
. 6分
(2)方法一:过点 作
作 ,垂足
,垂足 ,连接
,连接 .
.

在等边 中
中 ,
,
在等边 中
中 .
.
在 中
中 .
.

 是直角三角形,且
是直角三角形,且 ,故
,故 . 8分
. 8分
 、
、 平面
平面 ,
, .
.

 平面
平面 . 又
. 又 平面
平面 ,故
,故 .
.
 、
、 平面
平面 ,
,  ,故
,故 平面
平面 .
.
因为 平面
平面 ,所以
,所以 .
.
所以 是二面角
是二面角 的平面角. 10分
的平面角. 10分
在 中,
中, .
.
在 中,
中, .
.

 .
.
所以二面角 的余弦值
的余弦值 . 13分
. 13分
方法二:在等边 中
中 ,在等边
,在等边 中
中 .
.
在 中
中 .
.

 是直角三角形,且
是直角三角形,且 ,故
,故 . 8分
. 8分
分别以 ,
, ,
, 为
为 轴,
轴, 轴,
轴, 轴建立如图空间直角坐标系
轴建立如图空间直角坐标系 ,
,

由已知得 ,
, ,
, ,
, .
.
设 为平面
为平面 的法向量,
的法向量,
则 ,
, ,
,
 ,
, ,
,
又 ,
, ,
,
 .
.
取 ,则
,则 ,
, ,故
,故 . 11分
. 11分
又 是平面
是平面 的法向量,二面角
的法向量,二面角 的大小等于
的大小等于 或其补角.
或其补角.

 .
.
依图知二面角 的余弦值为
的余弦值为 .. 13分
.. 13分
考点:线线垂直、线面垂直、二面角.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 中,
中, ,
, ,
, ,则
,则 边上的高为( )
边上的高为( ) B.
B.
 D.
D.
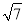 ,BC=2,B=60°,则BC边上的高等于( )
,BC=2,B=60°,则BC边上的高等于( )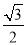 B.
B.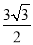 C.
C.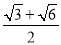 D.
D.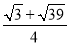

 B.
B. C.
C. D.
D.
 在复平面内对应的点的坐标为( )
在复平面内对应的点的坐标为( ) B.
B. C.
C. D.
D.
 ,
, 满足约束条件
满足约束条件 ,则
,则 的最大值是 .
的最大值是 . ,
, ,
, ,则( )
,则( ) B.
B. C.
C. D.
D.
 的图象向右平移
的图象向右平移 个单位长度后得到函数
个单位长度后得到函数 的图象,若
的图象,若 的图象都经过点
的图象都经过点 ,则
,则 的值可以是
的值可以是 B.
B. C.
C. D.
D.
 ,则
,则 的大小关系为( )
的大小关系为( ) B.
B. C.
C. D.
D.