题目内容
已知函数f（x）＝
+m+1对x∈（0，
）的图象恒在x轴上方，则m的取值范围是 （ ）
A．2－2
＜m＜2+2 B．m＜2
C． m＜2+2 D．m≥2+2
解：法1：令t＝
，则问题转化为函数f（t）＝t2－mt+m+1对t∈（1，）的图象恒在x轴的上方，即△＝（－m）2－4（m+1）＜0或 
解得m＜2+2．
法2：问题转化为m＜
，t∈（1，），即m比函数y＝ ，t∈（1，）的最小值还小，又y＝＝t－1+
+2≥2
+2＝2+2，所以m＜2+2，选 C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
．
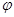）（ω＞0，0＜
＝
，且a∈（0，
），求f（a）的值．
－a
＋x（a＞0）．
＝
，求f（x）图像在x＝1处的切线的方程；
的极大值和极小值分别为m，n，证明：
．
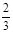与x＝1时都取得极值.
，若f（x）存在零点，则实数a的取值范围