题目内容
在等比数列{an}中，a3+a5=18，a9+a11=144，则a5+a8= ．
【答案】分析：先由已知条件求出公比以及首项的值，再代入所求即可得到答案．
解答：解：a3+a5=18，a9+a11=144，那么a1q2（1+q2）=18；
a1q8（1+q2）=144．
∴q6=8．
∴q2=2⇒q=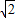
，q=-
．
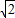所以a1=3．当q=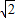
时，所以a5+a8=
．
当q=-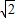
时，a5+a8=
．
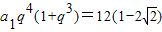故答案为：12（1±2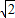
）．
点评：本题主要考查等比数列的性质应用．解决这一类型题目，一般是把已知条件都转化为用首项和公比表示，求出首项和公比即可求出结论．
解答：解：a3+a5=18，a9+a11=144，那么a1q2（1+q2）=18；
a1q8（1+q2）=144．
∴q6=8．
∴q2=2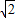⇒q=
，q=-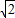．所以a1=3．当q=
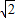时，所以a5+a8=．当q=-
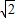时，a5+a8=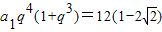．故答案为：12（1±2
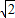）．点评：本题主要考查等比数列的性质应用．解决这一类型题目，一般是把已知条件都转化为用首项和公比表示，求出首项和公比即可求出结论．
练习册系列答案
阅读快车系列答案
相关题目
在等比数列{an}中，若a1=1，公比q=2，则a12+a22+…+an2=（ ）
| A、（2n-1）2 | ||
B、
| ||
| C、4n-1 | ||
D、
|