题目内容
设直线y=ax+b与双曲线3x2-y2=1交于A、B，且以AB为直径的圆过原点，求点P（a，b）的轨迹方程．
分析：将直线方程与双曲线方程消去y，可得（a2-3）x2+2abx+b2+1=0，利用根的判别式算出a2＜3．设A（x1，y1），B（x2，y2），利用根与系数的关系可得x1+x2=
，x1•x2=
．根据直径所对的圆周角为直角，结合题意得到
⊥
，所以x1x2+y1y2=0，代入前面的等式化为关于a、b的等式，化简得到a2-2b2=-1．由此即可得到点P（a，b）满足的轨迹方程．
| 2ab |
| 3-a2 |
| b2+1 |
| a2-3 |
| OA |
| OB |
解答：解：由
，
消去y得：（a2-3）x2+2abx+b2+1=0．
∵直线与双曲线交于A、B两点，
∴
，解得a2＜3．
设A（x1，y1），B（x2，y2），
可得x1+x2=
，x1•x2=
．
∴y1•y2=（ax1+b）（ax2+b）=a2x1x2+ab（x1+x2）+b2，
又∵以AB为直径的圆过原点，
∴
⊥
，得x1x2+y1y2=0，
由此可得x1x2+[a2x1x2+ab（x1+x2）+b2]=0，
即（1+a2）x1x2+ab（x1+x2）+b2=0，
可得：（1+a2）•
-ab•
+b2=0，化简得：a2-2b2=-1．
因此，点P（a，b）的轨迹方程为x2-2y2=-1，即2y2-x2=1（x2＜3）．
|
消去y得：（a2-3）x2+2abx+b2+1=0．
∵直线与双曲线交于A、B两点，
∴
|
设A（x1，y1），B（x2，y2），
可得x1+x2=
| 2ab |
| 3-a2 |
| b2+1 |
| a2-3 |
∴y1•y2=（ax1+b）（ax2+b）=a2x1x2+ab（x1+x2）+b2，
又∵以AB为直径的圆过原点，
∴
| OA |
| OB |
由此可得x1x2+[a2x1x2+ab（x1+x2）+b2]=0，
即（1+a2）x1x2+ab（x1+x2）+b2=0，
可得：（1+a2）•
| b2+1 |
| a2-3 |
| 2ab |
| 3-a2 |
因此，点P（a，b）的轨迹方程为x2-2y2=-1，即2y2-x2=1（x2＜3）．
点评：本题已知直线与双曲线相交得到弦AB，以AB为直径的圆过原点，求点P（a，b）满足的轨迹方程．着重考查了圆的性质、双曲线的标准方程与简单性质、直线与圆锥曲线的位置关系等知识，考查了一元二次方程根的判别式和根与系数的关系，属于中档题．
练习册系列答案
相关题目
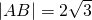，则a=________．
，则a= ．
，则a= ．