题目内容
(本题满分14分)
已知 内角
内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,其中
,其中 ,
, .
.
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)设 ,求
,求 的取值范围.
的取值范围.
已知
 内角
内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,其中
,其中 ,
, .
.(Ⅰ)若
 ,求
,求 的值;
的值;(Ⅱ)设
 ,求
,求 的取值范围.
的取值范围. (Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
 ;(Ⅱ)
;(Ⅱ) .
.本试题主要是考查了三角形中的正弦定理和余弦定理的运用,求解三角形的边角的关系的综合运用,以及三角恒等变换,三角函数值域的求解的综合问题。
(1)直接由正弦定理可知结论。
(2)利用余弦定理得到 ,然后结合由题知关于
,然后结合由题知关于 的一元二次方程应该有解,令
的一元二次方程应该有解,令 ,得
,得 得到角C的范围,从而得到结论。
得到角C的范围,从而得到结论。
解、(Ⅰ)由正弦定理得 ,∴
,∴ ………6分
………6分
(Ⅱ)在 中,由余弦定理得,
中,由余弦定理得, ,所以
,所以 ,即
,即 ,由题知关于
,由题知关于 的一元二次方程应该有解,令
的一元二次方程应该有解,令 ,得
,得 (舍去,因为
(舍去,因为 )或
)或 ,所以
,所以 .
.

 ,
,
∴ .…………………………………………………………………………14分
.…………………………………………………………………………14分
(1)直接由正弦定理可知结论。
(2)利用余弦定理得到
 ,然后结合由题知关于
,然后结合由题知关于 的一元二次方程应该有解,令
的一元二次方程应该有解,令 ,得
,得 得到角C的范围,从而得到结论。
得到角C的范围,从而得到结论。解、(Ⅰ)由正弦定理得
 ,∴
,∴ ………6分
………6分(Ⅱ)在
 中,由余弦定理得,
中,由余弦定理得, ,所以
,所以 ,即
,即 ,由题知关于
,由题知关于 的一元二次方程应该有解,令
的一元二次方程应该有解,令 ,得
,得 (舍去,因为
(舍去,因为 )或
)或 ,所以
,所以 .
.
 ,
,∴
 .…………………………………………………………………………14分
.…………………………………………………………………………14分
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
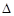 ABC中,已知
ABC中,已知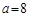 ,
,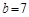 ,
,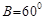 ,求
,求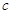 .
.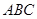 中,角
中,角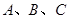 的对边分别为
的对边分别为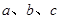 ,且
,且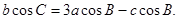
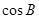 的值;
的值;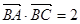 ,且
,且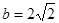 ,求
,求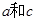 的值.
的值.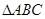 中,
中,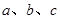 分别为角
分别为角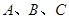 所对的三边,已知
所对的三边,已知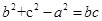 .
.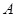 的值;
的值;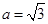 ,
,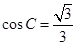 ,求
,求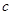 的长.
的长. ,则△ABC的形状是( )
,则△ABC的形状是( ) 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 ,
, .
.  ,求
,求 的值.
的值.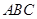 中,若
中,若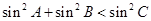 ,则△
,则△ 中,
中, ,
,
 ,则
,则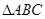 的三个内角
的三个内角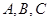 所对的边分别是
所对的边分别是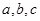 ,且
,且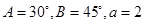 ,则
,则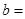 .
.