题目内容
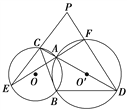
【题目】已知椭圆![]() :
: ![]() 的左焦点
的左焦点![]() ,若椭圆上存在一点
,若椭圆上存在一点![]() ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段![]() 相切于线段
相切于线段![]() 的中点
的中点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过坐标原点![]() 的直线交椭圆
的直线交椭圆![]() :
: ![]() 于
于![]() 、
、![]() 两点,其中点
两点,其中点![]() 在第一象限,过
在第一象限,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连结
,连结![]() 并延长交椭圆
并延长交椭圆![]() 于
于![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:
(Ⅰ)连接![]() ,由题设条件能够推导出
,由题设条件能够推导出![]() ,在
,在![]() 中,
中, ![]() ,由此能求出椭圆
,由此能求出椭圆![]() 的方程.(Ⅱ)由(Ⅰ)得椭圆
的方程.(Ⅱ)由(Ⅰ)得椭圆![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,并代入
,并代入![]() 得:
得: ![]() ,利用根的判别式、中点坐标公式推导出当
,利用根的判别式、中点坐标公式推导出当![]() ,或
,或![]() ,或
,或![]() 时,直线
时,直线![]() 过椭圆
过椭圆![]() 的顶点.(Ⅲ)法一:由椭圆
的顶点.(Ⅲ)法一:由椭圆![]() 的方程为
的方程为![]() ,设
,设![]() ,则
,则![]() ,直线
,直线![]() 的方程为
的方程为![]() ,过点
,过点![]() 且与
且与![]() 垂直的直线方程为
垂直的直线方程为![]() ,由此能够证明
,由此能够证明![]() .法二:由(Ⅰ)得椭圆
.法二:由(Ⅰ)得椭圆![]() 的方程为
的方程为![]() ,设
,设![]() ,则
,则![]() ,故
,故![]() ,由此能够证明
,由此能够证明![]() .
.
试题解析:
解:(Ⅰ)连接![]() 为原点,
为原点, ![]() 为右焦点),由题意知:椭圆的右焦点为
为右焦点),由题意知:椭圆的右焦点为![]()
因为![]() 是
是![]() 的中位线,且
的中位线,且![]() ,所以
,所以![]()
所以![]() ,故
,故![]()
在![]() 中,
中, ![]()
即![]() ,又
,又![]() ,解得
,解得![]()
所求椭圆![]() 的方程为
的方程为![]() .---------6分
.---------6分
(Ⅱ)法一:由(Ⅰ)得椭圆![]() 的方程为
的方程为![]()
根据题意可设![]() ,则
,则![]()
则直线![]() 的方程为
的方程为![]() …①
…①
过点![]() 且与
且与![]() 垂直的直线方程为
垂直的直线方程为![]() …②
…②
①![]() ②并整理得:
②并整理得: ![]()
又![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]()
所以![]()
即①、②两直线的交点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() .
.
法二:由(Ⅰ)得椭圆![]() 的方程为
的方程为![]()
根据题意可设![]() ,则
,则![]() ,
, ![]() ,
, ![]()
所以直线![]()
 ,化简得
,化简得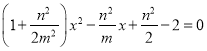
所以![]()
因为![]() ,所以
,所以![]() ,则
,则![]()
所以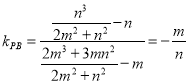 ,则
,则![]() ,即
,即![]() .
.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目