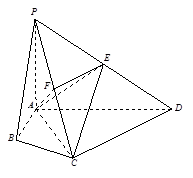题目内容
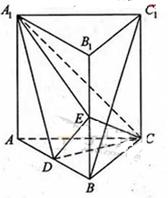
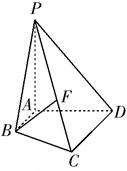
如图,在四棱锥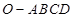 中,底面
中,底面 是边长为
是边长为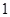 的菱形,
的菱形,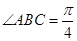 ,
, 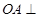 底面
底面 ,
,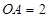 ,
,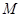 为
为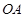 的中点,
的中点,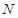 为
为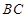 的中点.
的中点.
(Ⅰ)求四棱锥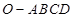 的体积;
的体积;
(Ⅱ)证明:直线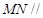 平面
平面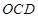 .
.
(Ⅰ)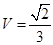 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)求四棱锥 的体积,由体积公式
的体积,由体积公式 ,由已知
,由已知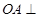 底面
底面 ,显然
,显然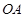 是高,且值为2,而底面是边长为
是高,且值为2,而底面是边长为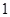 的菱形,
的菱形,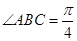 ,,有平面几何知识,可求得面积
,,有平面几何知识,可求得面积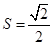 ,代入公式,可求得体积;(Ⅱ)证明:直线
,代入公式,可求得体积;(Ⅱ)证明:直线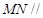 平面
平面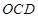 ,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,本题虽有中点,但没直接的三角形,可考虑用平行四边形的对边平行,可取OD的中点G,连结CG,MG,证明四边形
,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,本题虽有中点,但没直接的三角形,可考虑用平行四边形的对边平行,可取OD的中点G,连结CG,MG,证明四边形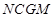 为平行四边形即可,也可取
为平行四边形即可,也可取 中点
中点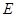 ,连接
,连接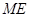 ,
,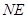 ,利用面面平行则线面平行,证平面
,利用面面平行则线面平行,证平面 平面
平面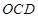 即可.
即可.
试题解析:(Ⅰ)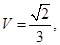
(Ⅱ)取 中点
中点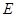 ,连接
,连接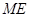 ,
,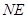 ,
,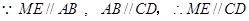 ,又
,又
 ,
, .
.
考点:几何体的体积,线面平行的判断.

练习册系列答案
相关题目

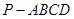 中,底面
中,底面 是边长为1的正方形,
是边长为1的正方形,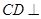 平面
平面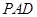 ,
, 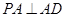 ,
,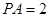 ,
,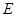 为
为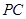 的中点,
的中点,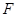 在棱
在棱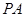 上.
上.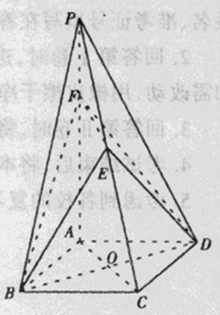
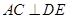 ;
;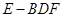 的体积.
的体积.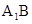 的中点,F在棱CC1上。
的中点,F在棱CC1上。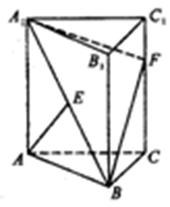
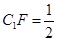 CF时,求多面体ABCFA1的体积;
CF时,求多面体ABCFA1的体积; ),
),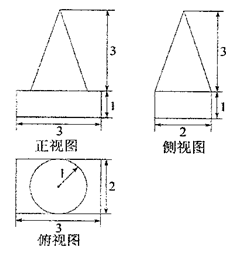
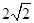 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积. 的底面是正方形,
的底面是正方形, 底面
底面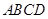 ,
,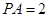 ,
, ,点
,点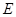 、
、 分别为棱
分别为棱 、
、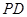 的中点.
的中点.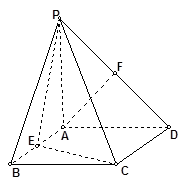
 平面
平面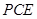 ;
;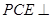 平面
平面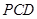 ;
;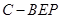 的体积.
的体积.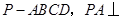 平面
平面 ,底面
,底面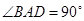 ,且
,且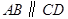 ,
,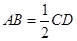 .
.
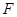 在线段
在线段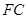 上运动,且设
上运动,且设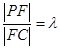 ,问当
,问当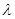 为何值时,
为何值时,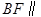 平面
平面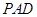 ,并证明你的结论;
,并证明你的结论;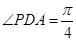 ,
,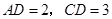 求四棱锥
求四棱锥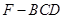 的体积.
的体积.