题目内容
已知A、B、C、D四点的坐标分别为A(1,0)、B(4,3)、C(2,4)、D(m,n).当m、n满足什么条件时,四边形ABCD分别是平行四边形、菱形、矩形、正方形、梯形(A、B、C、D按逆时针方向排列)?
解:由条件知![]() =(3,3),
=(3,3),![]() =(-2,1),AD=(m-1,n),
=(-2,1),AD=(m-1,n),![]() =(2-m,4-n).
=(2-m,4-n).
(1)若四边形ABCD为平行四边形,则![]() ,∴(3,3)=(2-m,4-n),解得m=-1,n=1.
,∴(3,3)=(2-m,4-n),解得m=-1,n=1.
∴当m=-1,n=1时,四边形ABCD为平行四边形.
(2)当m=-1,n=1时,![]() =(3,3),
=(3,3),![]() =(-2,1).
=(-2,1).
则|![]() |=
|=![]() ,|
,|![]() |=
|=![]() ,|
,|![]() |≠|
|≠|![]() |.因此,使四边形ABCD为菱形的m、n不存在.
|.因此,使四边形ABCD为菱形的m、n不存在.
(3)当m=-1,n=1时,![]() ·
·![]() =(3,3)·(-2,1)=-3≠0,即AB、CD不垂直.因此使四边形ABCD为距形的m、n不存在.
=(3,3)·(-2,1)=-3≠0,即AB、CD不垂直.因此使四边形ABCD为距形的m、n不存在.
(4)由(2)、(3)知,使四边形ABCD为正方形的m、n不存在.
(5)若四边形ABCD为梯形,则![]() =λ
=λ![]() 或
或![]() =λ
=λ![]() ,其中λ为实数,且λ>0,λ≠1.
,其中λ为实数,且λ>0,λ≠1.
所以![]() (λ>0,λ≠1)或
(λ>0,λ≠1)或![]() (λ>0,λ≠1).
(λ>0,λ≠1).
整理得m、n的取值条件为n=m+2(m<2,m≠-1)或n=![]() (m<1,m≠-1).
(m<1,m≠-1).

练习册系列答案
相关题目
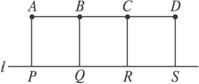
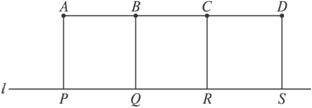
 如图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )
如图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )