题目内容
2![]()
|
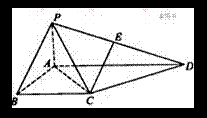 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形, ∠ABC=∠BAD=90°,![]() .
.
(1)求证:平面PAC⊥平面PCD;
(2)在棱PD上是否存在一点E,使CE//平面PAB?
若存在,请确定E点的位置;若不存在,请说明理由.
(1) (2)棱PD上存在点E,且E为PD中点,使CE//面PAB
解析:
设PA=1(I)由题意PA=BC=1,AD=2
![]()
由勾股定理得AC⊥CD又∵PA⊥面ABCD CD![]() 面ABCD
面ABCD
∴PA⊥CD,PA∩AC=A,∴CD⊥面PAC,又CD![]() 面PCD,
面PCD,
∴面PAC⊥面PCD
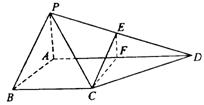
(II)证明:作CF//AB交AD于F,作EF//AP交PD于E,连接CE
∵CF//AB EF//PA CF∩EF=F PA∩AB=A
|
CE//平面PAB![]()
∴F为AD的中点,∴E为PD中点
故棱PD上存在点E,且E为PD中点,使CE//面PAB

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,求PD的长。
,求PD的长。