题目内容
(本题满分13分)
已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,过
两点,过![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() ,垂足为
,垂足为![]() .
.
(1)设![]() 点的坐标为
点的坐标为![]() ,求
,求![]() 的最值;
的最值;
(2)求四边形![]() 的面积的最小值.
的面积的最小值.
解析:(1)由已知得![]() (-2,0),
(-2,0),![]() (2,0),P
(2,0),P![]() ⊥P
⊥P![]() ,
,
∴P![]() 满足
满足![]() , ……………………1分
, ……………………1分
∴![]() ,∴
,∴![]() =
=![]() , ……………2分
, ……………2分
∴它的最小值为![]() ,最大值为
,最大值为![]() . ………………………3分
. ………………………3分
(2)若直线![]() 的斜率
的斜率![]() 存在且不为0,因
存在且不为0,因![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() . ………………………4分
. ………………………4分
联立![]() 和
和![]() ,消去
,消去![]() 得:
得:![]() ,
,![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() =
=![]() ; ………………………………7分
; ………………………………7分
联立![]() 和
和![]() ,消去
,消去![]() 得:
得:![]() ,
,![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() =
=![]() ; ………………………………9分
; ………………………………9分
 =
=![]() ,
,
当![]() 时等号成立. ……………………………11分
时等号成立. ……………………………11分
当![]() 为0或不存在时,
为0或不存在时,![]()
![]() ; ………………12分
; ………………12分
综上,四边形![]() 的面积的最小值为
的面积的最小值为![]() . ………………13分
. ………………13分

练习册系列答案
相关题目
 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.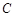 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.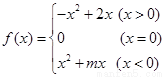 为奇函数;
为奇函数;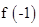 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
 取得最小值时点P的坐标.
取得最小值时点P的坐标.  是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆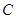 于
于 两点
两点 ,求直线
,求直线 的方程;
的方程; 恒过一定点.
恒过一定点.