题目内容
数列 满足
满足
 ,且
,且 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 若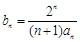 ,设数列
,设数列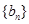 的前
的前 项和为
项和为 ,求证:
,求证: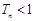 .
.
(1) ;(2)详见解析.
;(2)详见解析.
解析试题分析:本小题主要通过递推数列通项公式的求取,考查对考生的运算求解能力、逻辑推理能力,对考生化归与转化的数学思想提出较高要求. 本题属于基础试题,难度相对较低.(1)采用构造数列的思路进行分析,借助将递推式两边同时除以 达到目的;(2)采用裂项相消法求解数列
达到目的;(2)采用裂项相消法求解数列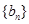 的前
的前 项和为
项和为 ,进而借助放缩法进行不等式的证明.
,进而借助放缩法进行不等式的证明.
试题解析:(1) 由 可知
可知 ,
,
所以数列 是公差为1的等差数列.
是公差为1的等差数列.
由等差数列的通项公式可知, .
.
所以 . (6分)
. (6分)
(2) 由(1)可得 ,
,
则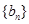 的前
的前 项和
项和 . (12分)
. (12分)
考点:(1)数列的通项公式;(2)数列求和;(3)不等式的证明.

练习册系列答案
相关题目
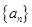 的前
的前 项和
项和 满足
满足 ,其中
,其中 .
. ,求
,求 及
及 ;
; ,求证:
,求证: ,并给出等号成立的充要条件.
,并给出等号成立的充要条件. (
( 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前 型数列。
型数列。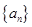 是首项
是首项 的
的 的值;
的值; 是
是 试求
试求 与
与 的递推关系,并证明
的递推关系,并证明 对
对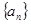 的前
的前 项和为
项和为 ,首项
,首项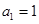 ,点
,点 在曲线
在曲线 上.
上. ;
; 的通项公式
的通项公式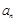 ;
; ,
, 表示数列
表示数列 的前项和,若
的前项和,若 恒成立,求
恒成立,求 的取值范围.
的取值范围. 的前
的前 项和
项和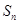 ,满足:
,满足: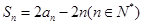 .
.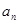 ;
;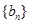 的满足
的满足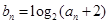 ,
,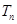 为数列
为数列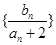 的前
的前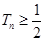 .
. 的前
的前 项和为
项和为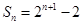 ,数列
,数列 是首项为
是首项为 ,公差为
,公差为 的等差数列,且
的等差数列,且 成等比数列.
成等比数列. ,求数列
,求数列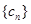 的前
的前 .
. 的前
的前 项和为
项和为 ,若
,若 ,
, ,
, .
.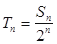 ,
, ;
; ,求
,求 的取值范围.
的取值范围. 的前
的前 项和为
项和为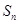 ,对任意的
,对任意的 ,都有
,都有 ,且
,且 ;数列
;数列 满足
满足 .
. 的值及数列
的值及数列 的通项公式;
的通项公式; 对一切
对一切 成立.
成立. 的前
的前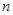 项和为
项和为 ,且对任意的
,且对任意的 都有
都有 ,
,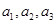 ;
; ,并用数学归纳法证明
,并用数学归纳法证明