题目内容
若正数项数列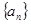 的前
的前 项和为
项和为 ,首项
,首项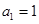 ,点
,点 在曲线
在曲线 上.
上.
(1)求 ;
;
(2)求数列 的通项公式
的通项公式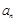 ;
;
(3)设 ,
, 表示数列
表示数列 的前项和,若
的前项和,若 恒成立,求
恒成立,求 及实数
及实数 的取值范围.
的取值范围.
(1) ,
, .;(2)
.;(2) ;(3)
;(3)
 ,
, .
.
解析试题分析:(1)分别取 和
和 ,可求;(2)将点P代入曲线方程,化简,可得:
,可求;(2)将点P代入曲线方程,化简,可得: ,从而数列
,从而数列 是以
是以 为首项,1为公差的等差数列,可求得
为首项,1为公差的等差数列,可求得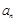 ;(3)用裂项相消法可求解.
;(3)用裂项相消法可求解.
试题解析:(1)因为点 在曲线
在曲线 上,所以
上,所以 .
.
分别取 和
和 ,得到
,得到 ,
,
由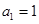 解得
解得 ,
, .
.
(2)由 得
得 .
.
所以数列 是以
是以 为首项,1为公差的等差数列
为首项,1为公差的等差数列
所以 , 即
, 即
由公式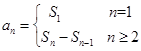 ,得
,得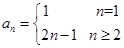
所以
(3)因为 ,所以
,所以 ,
,



显然 是关于
是关于 的增函数, 所以
的增函数, 所以 有最小值
有最小值
由于 恒成立,所以
恒成立,所以 ,
,
于是 的取值范围为
的取值范围为 .
.
考点:(1)数列前n项和与通项公式之间的关系;(2)等差数列的证明,等差数列的通项公式;(3)裂项相消法.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 满足
满足 ,则称数列
,则称数列 中,
中, ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中 为正整数.
为正整数. 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列;
为等比数列; 项积为
项积为 ,即
,即 ,求
,求 ;
; ,求数列
,求数列 的前
的前 ,并求使
,并求使 的
的 中,
中, (
( ).
). 的值;
的值; ,使得数列
,使得数列 是一个等差数列?若存在,求
是一个等差数列?若存在,求 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由. 的前
的前 项和为
项和为 ,
, ,
, 是
是 与
与 的等差中项(
的等差中项( ).
). 为等比数列;
为等比数列; ,使不等式
,使不等式 (
( 是正数组成的数列,
是正数组成的数列, .若点
.若点 在函数
在函数 的导函数
的导函数 图像上.
图像上. ,是否存在最小的正数
,是否存在最小的正数 ,使得对任意
,使得对任意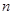
 都有
都有 成立?请说明理由.
成立?请说明理由. 且
且
 满足
满足
 ,且
,且 .
.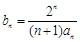 ,设数列
,设数列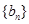 的前
的前 项和为
项和为 ,求证:
,求证: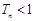 .
. 中,
中, ,
, ,若数列
,若数列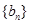 满足
满足 .
. 在函数
在函数 图象上,过点
图象上,过点 的切线的方向向量为
的切线的方向向量为 (
( >0).
>0). 的通项公式
的通项公式 ≤Sn对任意正整数n均成立,求实数
≤Sn对任意正整数n均成立,求实数