题目内容
已知球O的半径为4,圆M与圆N为该球的两个小圆,AB为圆M与圆N的公共弦,AB=4,OM=ON=a,则两圆的圆心距|MN|的最大值为( )
| A.3 | B.2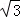 | C.3 | D.6 |
B
解析

练习册系列答案
相关题目
已知 ,
, .若
.若 是
是 的充分非必要条件,则实数
的充分非必要条件,则实数 的取值范围是( )
的取值范围是( )
A.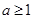 | B. | C. | D. |
直线 与圆
与圆 相交所得线段的长度为 ( )
相交所得线段的长度为 ( )
A. | B. | C. | D. |
圆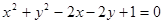 上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )
| A.2 | B.1+ | C. | D.1+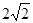 |
直线tx+y-t+1=0(t∈R)与圆x2+y2-2x+4y-4=0的位置关系为( )
| A.相交 | B.相切 | C.相离 | D.以上都有可能 |
若直线3x+y+a=0过圆x2+y2+2x-4y=0的圆心,则a的值为( )
| A.-1 | B.1 | C.3 | D.-3 |
 在点
在点 处的切线为
处的切线为 ,则直线
,则直线 上的任意点Q之间的最近距离是( )
上的任意点Q之间的最近距离是( )


 的正△
的正△ 沿边长为
沿边长为 的正方形
的正方形 的各边内侧逆时针方向滚动.当△
的各边内侧逆时针方向滚动.当△ 的轨迹长度是( )
的轨迹长度是( )



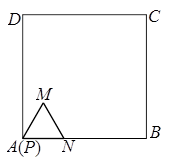
 ,0)引直线l与曲线
,0)引直线l与曲线 相交于A、B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于 ( )
相交于A、B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于 ( ) B.
B. C.
C. D.
D.