题目内容
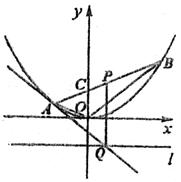
如图，一条抛物线与x轴相交于A、B两点，其顶点P在折线C-D-E上移动，若点C、D、E的坐标分别为（-1，4）、（3，4）、（3，1），点B的横坐标的最小值为1，则点A的横坐标的最大值为（ ）分析：先确定点B的横坐标的最小时抛物线的解析式，再确定点A的横坐标的最大时抛物线的解析式，由此可求点A的横坐标的最大值．
解答：解：∵抛物线的点P在折线C-D-E上移动，且点B的横坐标的最小值为1，
∴观察可知，当点B的横坐标的最小时，点P与点C重合．
∵C（-1，4），∴设当点B的横坐标的最小时抛物线的解析式为y=a（x+1）2+4．
∵B（1，0），∴0=4a+4，∴a=-1．
∴当点B的横坐标的最小时抛物线的解析式为y=-（x+1）2+4．
∵观察可知，当点A的横坐标的最大时，点P与点E重合，E（3，1），
∴当点A的横坐标的最大时抛物线的解析式为y=-（x-3）2+1．
令y=0，即-（x-3）2+1=0，解得x=2或x=4．
∵点A在点B的左侧，∴此时点A横坐标为2
∴点A的横坐标的最大值为2．
故选C．
∴观察可知，当点B的横坐标的最小时，点P与点C重合．
∵C（-1，4），∴设当点B的横坐标的最小时抛物线的解析式为y=a（x+1）2+4．
∵B（1，0），∴0=4a+4，∴a=-1．
∴当点B的横坐标的最小时抛物线的解析式为y=-（x+1）2+4．
∵观察可知，当点A的横坐标的最大时，点P与点E重合，E（3，1），
∴当点A的横坐标的最大时抛物线的解析式为y=-（x-3）2+1．
令y=0，即-（x-3）2+1=0，解得x=2或x=4．
∵点A在点B的左侧，∴此时点A横坐标为2
∴点A的横坐标的最大值为2．
故选C．
点评：本题考查抛物线的方程，考查学生分析解决问题的能力，确定抛物线的解析式是关键．
练习册系列答案
相关题目
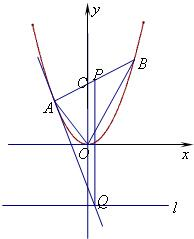如图，在平面直角坐标系xOy中，过y轴正方向上一点C（0，c）任作一直线，与抛物线y=x2相交于AB两点，一条垂直于x轴的直线，分别与线段AB和直线l：y=-c交于P，Q，
如图，一条抛物线与x轴相交于A、B两点，其顶点P在折线C-D-E上移动，若点C、D、E的坐标分别为（-1，4）、（3，4）、（3，1），点B的横坐标的最小值为1，则点A的横坐标的最大值为
·
=2，求c的值；