题目内容
(本小题满分14分)
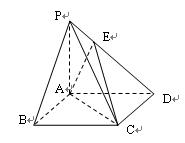
如图8,在直角梯形 中,
中, ,
, ,且
,且 .现以
.现以 为一边向形外作正方形
为一边向形外作正方形 ,然后沿边
,然后沿边 将正方形
将正方形 翻折,使平面
翻折,使平面 与平面
与平面 互相垂直,如图9.
互相垂直,如图9.
(1)求证:平面 平面
平面 ;
;
(2)求平面 与平面
与平面 所成锐二面角的大小.
所成锐二面角的大小.
证明(1)(法一)因为平面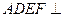 平面
平面 ,
,
且平面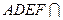 平面
平面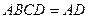 ,
,
又在正方形 中,
中,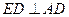 ,
,
所以,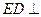 平面
平面 . ………………2分
. ………………2分
而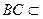 平面
平面 ,
,
所以,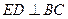 . ………………3分
. ………………3分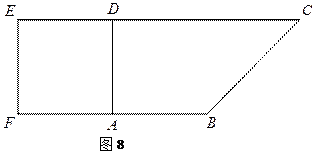
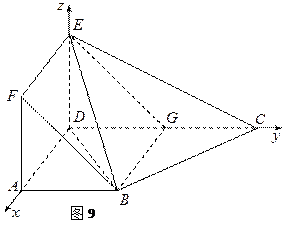
在直角梯形 中,
中, 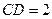 ,
,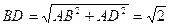 ,
, 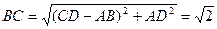 ,
,
所以,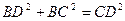 ,
,
所以,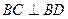 . ………………4分
. ………………4分
又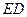 ,
,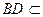 平面
平面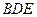 ,
,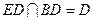 ,
,
所以,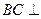 平面
平面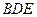 . ………………6分
. ………………6分
而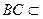 平面
平面 ,
,
所以,平面 平面
平面 . ……………7分
. ……………7分
(法二)同法一,得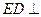 平面
平面 . …………………………2分
. …………………………2分
以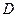 为原点,
为原点,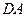 ,
,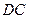 ,
,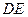 分别为
分别为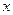 ,
,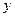
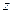 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.
则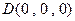 ,
,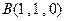 ,
,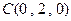 ,
,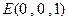 . …………………………3分
. …………………………3分
所以,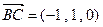 ,
, 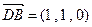 ,
,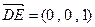 ,
,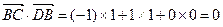 ,
,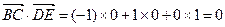 ,
,
所以,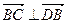 ,
,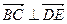 . …………………………………5分
. …………………………………5分
又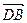 ,
,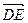 不共线,
不共线,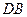 ,
,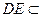 平面
平面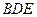 ,
,
所以,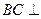 平面
平面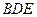 . …………………………6分
. …………………………6分
而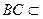 平面
平面 ,
,
所以,平面 平面
平面 . …………………………7分
. …………………………7分
(2)(法一)因为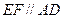 ,
,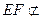 平面
平面 ,
,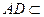 平面
平面 ,
,
所以,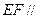 平面
平面 .
.
解析

练习册系列答案
相关题目
若直线 与
与 的交点在第一象限内,则
的交点在第一象限内,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知点(3,1)和(-4,6)在直线 的两侧则
的两侧则 的取值范围是( )
的取值范围是( )
| A.a<-7,或 a>24 | B.a=7或 24 | C.-7<a<24 | D.-24<a<7 |
 ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.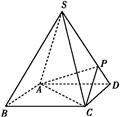
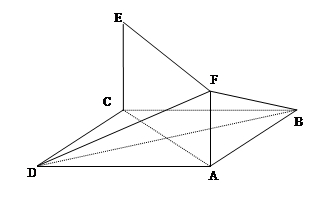
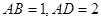 ,
,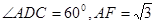
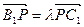 ,当 B1D⊥面PMN时,求
,当 B1D⊥面PMN时,求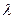 的值.
的值.
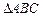 是边长为2的等边三角形,
是边长为2的等边三角形,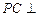 平面
平面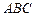 ,
,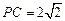 ,
,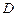 是
是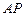 上一动点.
上一动点.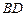 与平面
与平面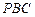 所成的角的正弦值;
所成的角的正弦值;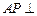 平面
平面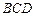 ?请说明理
?请说明理 由.
由.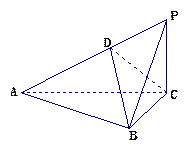
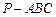 中,
中,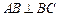 ,
,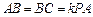 ,点
,点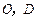 分别是
分别是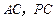 的中点,
的中点,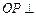 底面
底面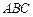 .
.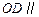 平面
平面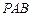 ;
;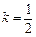 时,求直线
时,求直线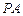 与平面
与平面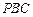 所成角的正弦值;
所成角的正弦值;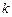 为何值时,
为何值时,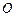 在平面
在平面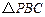 的重心.
的重心.
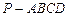 中,底面
中,底面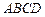 是边长为2的正方形,
是边长为2的正方形,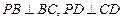 ,且
,且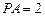 ,点
,点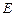 满足
满足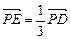 .
.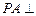 平面
平面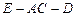 的余弦值;
的余弦值;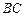 上是否存在点
上是否存在点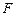 使得
使得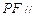 平面
平面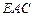 ?若存在,确定点
?若存在,确定点