题目内容
18.四棱锥P-ABCD中,底面ABCD是正方形,边长为a,PD=a,PA=PC=$\sqrt{2}$a,(1)求证:PD⊥平面ABCD;
(2)求证,直线PB与AC垂直.
分析 (1)通过PD2+DA2=PA2,证明PD⊥DA,PD⊥DC,即可证明PD⊥平面ABCD.
(2)连结BD,证明PD⊥AC,推出AC⊥平面PDB,然后说明PB与AC所成的角为90°,得到结果.
解答 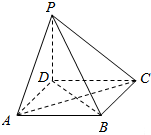 (本小题满分12分)
(本小题满分12分)
(1)证明:∵PD=a,AD=a,PA=$\sqrt{2}$a,
∴PD2+DA2=PA2,同理∴∠PDA=90°.
即PD⊥DA,PD⊥DC,
∵AO∩DC=D,
∴PD⊥平面ABCD.
(2)证明:连结BD,∵ABCD是正方形,
∴BD⊥AC,
∵PD⊥平面ABCD,
∴PD⊥AC,
∵PD∩BD=D
∴AC⊥平面PDB,
∵PB?平面PDB,
∴AC⊥PB,
∴PB与AC所成的角为90°,
∴直线PB与AC垂直.
点评 本题考查直线与平面垂直的判定定理的应用,直线与平面垂直的性质定理的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.若y=f(x)为R上的减函数,z=af(x)为R上的增函数,则实数a的值为( )
| A. | a<0 | B. | a>0 | C. | a≤0 | D. | a为任意实数 |
10.已知狆:p:$\frac{1}{{x}-2}$≥1,q:|x-a|<1,若p是q的充分不必要条件,则实数a的取值范围为( )
| A. | (-∞,3] | B. | [2,3] | C. | (2,3] | D. | (2,3) |
7.为了得到函数y=$\frac{1}{2}$cos(2x+$\frac{π}{3}$)的图象,可以把函数y=$\frac{1}{2}$cos2x的图象上所有的点( )
| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |