题目内容

任意正整数n都可以表示为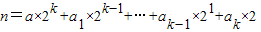

的形式，其中a=1，当1≤i≤k时，a₁=0或a_i=1．现将等于0的a_f的总个数记为f（n）（例如：l=l×2，4=l×2²+0×2¹十0×2，从而f（1）=0，f（4）=2．由此可以计算求得

= ．

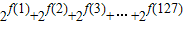【答案】分析：先列出如表所示，通过分析、猜想、归纳出其规律，进而可计算出其和．
解答：解：列表如下：

由表格可得到如下规律：正整数k从2ⁿ到2ⁿ⁺¹-1，则∑2^f（k）=3^n-1．
因此：

=3+3¹+3²+3³+3⁴+3⁵+3⁶
=

=1093．
故答案为1093．
点评：通过列表找出其规律是解题的关键．

练习册系列答案

同步练习强化拓展系列答案

任意正整数n都可以表示为 $数学公式$ 的形式，其中a₀=1，当1≤i≤k时，a₁=0或a_i=1．现将等于0的a_f的总个数记为f（n）（例如：l=l×2⁰，4=l×2²+0×2¹十0×2⁰，从而f（1）=0，f（4）=2．由此可以计算求得 $数学公式$ =________．

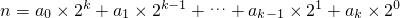任意正整数n都可以表示为的形式，其中a0=1，当1≤i≤k时，a1=0或ai=1．现将等于0的af的总个数记为f（n）（例如：l=l×20，4=l×22+0×21十0×20，从而f（1）=0，f（4）=2．由此可以计算求得=________．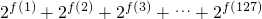