题目内容
集合E={x||x-1|≥m}，F={x
＞1}.(Ⅰ)若m=3，求E∩F；
(Ⅱ)若E∩F=
，求实数m的取值范围．
答案：解：(Ⅰ)m=3时，E={x||x-1|≥3}={x|x≤-2或x≥4}，
F={x|＞1}={x|＜0}={x|-6＜x＜4}．
∴E∩F={x|x≤-2或x≥4}{x|-6＜x＜4}={x|-6＜x≤2}．
(Ⅱ)∵E={x||x-1|≥m}，
①m≤0时，E=R，E∩F=F
，不满足条件．
②m＞0时，E={x|x≤1-m或x≥1+m}，
由E∩F=
，F={x|-6＜x＜4}，
∴
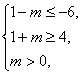解得m≥7．
∴综上，实数m的取值范围为m≥7．
练习册系列答案
相关题目