题目内容
已知椭圆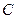 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在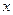 轴上,离心率为
轴上,离心率为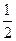 ,椭圆
,椭圆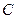 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为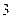 .
.
(Ⅰ)求椭圆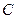 的标准方程;
的标准方程;
(Ⅱ)若过点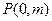 的直线
的直线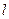 与椭圆
与椭圆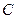 交于不同的两点
交于不同的两点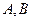 ,且
,且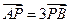 ,求实数
,求实数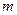 的取值范围.
的取值范围.
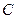 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在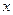 轴上,离心率为
轴上,离心率为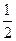 ,椭圆
,椭圆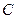 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为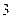 .
.(Ⅰ)求椭圆
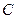 的标准方程;
的标准方程;(Ⅱ)若过点
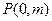 的直线
的直线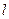 与椭圆
与椭圆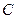 交于不同的两点
交于不同的两点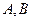 ,且
,且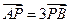 ,求实数
,求实数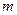 的取值范围.
的取值范围.解:(Ⅰ)设所求的椭圆方程为:
由题意:
所求椭圆方程为: . ……………………5分
. ……………………5分
(Ⅱ)若过点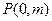 的斜率不存在,则
的斜率不存在,则 .
.
若过点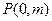 的直线斜率为
的直线斜率为 ,即:
,即: 时,
时,
直线 的方程为
的方程为
由

因为 和椭圆
和椭圆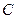 交于不同两点
交于不同两点
所以 ,
,
所以 ①
①
设
由已知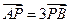 ,则
,则 ②
②

 ③
③
将③代入②得:
整理得:
所以 代入①式得
代入①式得
 ,解得
,解得 .
.
所以 或
或 .
.
综上可得,实数 的取值范围为:
的取值范围为: .
.
……………………14分

由题意:

所求椭圆方程为:
 . ……………………5分
. ……………………5分(Ⅱ)若过点
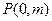 的斜率不存在,则
的斜率不存在,则 .
.若过点
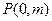 的直线斜率为
的直线斜率为 ,即:
,即: 时,
时,直线
 的方程为
的方程为
由


因为
 和椭圆
和椭圆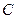 交于不同两点
交于不同两点所以
 ,
,
所以
 ①
①设

由已知
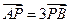 ,则
,则 ②
②
 ③
③将③代入②得:

整理得:

所以
 代入①式得
代入①式得
 ,解得
,解得 .
.所以
 或
或 .
.综上可得,实数
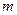 的取值范围为:
的取值范围为: .
.……………………14分
略

练习册系列答案
相关题目
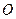 为坐标原点,
为坐标原点,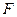 为椭圆
为椭圆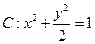 在
在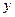 轴正半轴上的焦点,过
轴正半轴上的焦点,过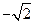 的直线
的直线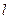 与
与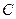 交与
交与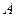 、
、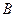 两点,点
两点,点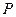 满足
满足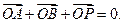
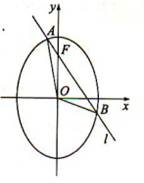
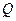 ,证明:
,证明: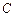 :
: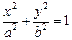 (
(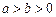 ),其焦距为
),其焦距为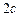 ,若
,若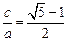 (
(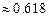 ),则称椭圆
),则称椭圆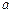 、
、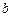 、
、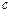 成等比数列.
成等比数列.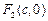 ,
,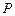 为椭圆
为椭圆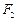 、
、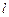 ,使
,使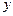 轴的交点
轴的交点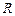 满足
满足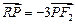 ?若存在,求直线
?若存在,求直线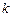 ;若不存在,请说明理由.
;若不存在,请说明理由.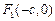 、
、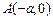 、
、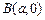 、
、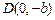 、
、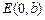 为顶点的菱形
为顶点的菱形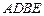 的内切圆过焦点
的内切圆过焦点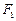 、
、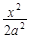 +
+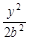 =1(a>b>0)与双曲线
=1(a>b>0)与双曲线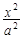 -
-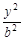 =1有相同的焦点,则椭圆的离心率为
=1有相同的焦点,则椭圆的离心率为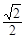

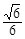
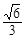
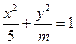 表示是焦点在y轴上的椭圆;q:三次函数
表示是焦点在y轴上的椭圆;q:三次函数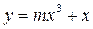
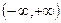 内单调递增,.求使“
内单调递增,.求使“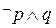 ”为真命题的实数m的取值范围.
”为真命题的实数m的取值范围.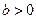 ,椭圆方程为
,椭圆方程为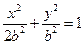 ,抛物线方程为
,抛物线方程为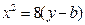 .如图所示,过点
.如图所示,过点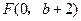 作
作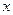 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为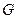 ,已知抛物线在点
,已知抛物线在点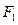 .
.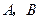 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点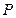 ,使得
,使得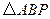 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).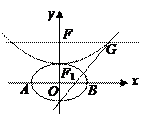
 ,过点
,过点 作抛物线
作抛物线
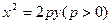 的切线
的切线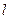 ,切点
,切点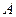 在第二象限,如图.(Ⅰ)求切点
在第二象限,如图.(Ⅰ)求切点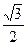 的椭圆
的椭圆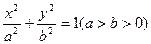 恰好经过切点
恰好经过切点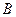 ,记切线
,记切线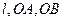 的斜率分别为
的斜率分别为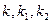 ,若
,若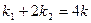 ,求椭圆方程.
,求椭圆方程.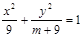 的离心率为
的离心率为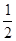 ,则m= ( )
,则m= ( )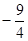
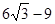
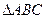 中,∠ABC=450,∠ACB=600,
中,∠ABC=450,∠ACB=600, ,记以AC为母线的圆锥为M2,m是圆锥M1任一母线,则圆锥M2的母线中与m垂直的直线有 ▲ 条
,记以AC为母线的圆锥为M2,m是圆锥M1任一母线,则圆锥M2的母线中与m垂直的直线有 ▲ 条