题目内容
抛物线y2=4x按向量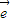 平移后的焦点坐标为 (3,2),则平移后的抛物线顶点坐标为( )
平移后的焦点坐标为 (3,2),则平移后的抛物线顶点坐标为( )A.(4,2)
B.(2,2)
C.(-2,-2)
D.(2,3)
【答案】分析:由于抛物线y2=4x的焦点坐标为F(1,0),顶点(0,0),而由F(1,0)按向量e 平移后的焦点坐标为 (3,2)可得平移向量 ,进而可求平移后的抛物线顶点坐标
,进而可求平移后的抛物线顶点坐标
解答:解:∵抛物线y2=4x的焦点坐标为F(1,0),顶点(0,0)
∵F(1,0)按向量e 平移后的焦点坐标为 (3,2)
∴
∴平移后的抛物线顶点坐标为(2,2)
故选:B
点评:本题主要考查了抛物线的性质的简单应用,向量平移的坐标表示,属于基础试题
 ,进而可求平移后的抛物线顶点坐标
,进而可求平移后的抛物线顶点坐标解答:解:∵抛物线y2=4x的焦点坐标为F(1,0),顶点(0,0)
∵F(1,0)按向量e 平移后的焦点坐标为 (3,2)
∴

∴平移后的抛物线顶点坐标为(2,2)
故选:B
点评:本题主要考查了抛物线的性质的简单应用,向量平移的坐标表示,属于基础试题

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
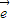 平移后的焦点坐标为 (3,2),则平移后的抛物线顶点坐标为( )
平移后的焦点坐标为 (3,2),则平移后的抛物线顶点坐标为( )