题目内容
已知点P的坐标是(-1,3),F是椭圆
+
=1的右焦点,点Q在椭圆上移动,|QF|+
|PQ|的最小值是( )
| x2 |
| 16 |
| y2 |
| 12 |
| 1 |
| 2 |
| A、8 | B、9 | C、10 | D、11 |
分析:由题意知e=
,右准线l:x=8,过Q作QQ′⊥l于Q′,分配P问题PP′⊥l于P′,|QF|+
|PQ|=
(|QQ′|+|P′Q|),由此可知当P‘与Q’重合时,可得|QF|+
|PQ|的最小值.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由题意知e=
,右准线l:x=8,
过Q作QQ′⊥l于Q′,分配P问题PP′⊥l于P′,
∵
=e=
,∴|QF|=
|QQ′|,
∴|QF|+
|PQ|=
(|QQ′|+|P′Q|),
当P‘与Q’重合时,|QF|+
|PQ|的最小值=8-(-1)=9.
故选B.
| 1 |
| 2 |
过Q作QQ′⊥l于Q′,分配P问题PP′⊥l于P′,
∵
| |QF| |
| |QQ′| |
| 1 |
| 2 |
| 1 |
| 2 |
∴|QF|+
| 1 |
| 2 |
| 1 |
| 2 |
当P‘与Q’重合时,|QF|+
| 1 |
| 2 |
故选B.
点评:本题考查直线和椭圆的位置关系,解题时要注意椭圆第二定义的合理运用.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
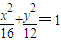 的右焦点,点Q在椭圆上移动,
的右焦点,点Q在椭圆上移动,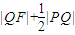 的最小值是( )
的最小值是( )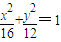 的右焦点,点Q在椭圆上移动,
的右焦点,点Q在椭圆上移动,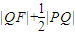 的最小值是( )
的最小值是( )