题目内容

函数f（x）=tan（2x-
π
3
）的单调递增区间是（　　）
A、[
kπ
2
-
π
12
，
kπ
2
+
5π
12
]（k∈Z）
B、（
kπ
2
-
π
12
，
kπ
2
+
5π
12
）（k∈Z）
C、（kπ+
π
6
，kπ+
2π
3
）（k∈Z）
D、[kπ-
π
12
，kπ+
5π
12
]（k∈Z）
分析：由正切函数的单调性的性质即可得到结论．
解答：解：由-
π
2
+kπ＜2x-
π
3
＜
π
2
+kπ，
即
kπ
2
-
π
12
＜x＜
kπ
2
+
5π
12
，（k∈Z），
故函数的单调性增区间为（
kπ
2
-
π
12
，
kπ
2
+
5π
12
）（k∈Z），
故选：B．
点评：本题主要考查正切函数的单调性的求解，利用正切函数的图象和性质是解决本题的关键．
练习册系列答案
相关题目
有以下四个命题：
①函数f（x）=sin（
π
3
-2x）的一个增区间是[
5π
12
，
11π
12
]；
②若函数f（x）=sin（ωx+φ）为奇函数，则φ为π的整数倍；
③对于函数f（x）=tan（2x+
π
3
），若f（x1）=f（x2），则x1-x2必是π的整数倍；
④函数y=2sin（2x+
π
3
）的图象关于点（
π
3
，0）对称．
其中正确的命题是
 
．（填上正确命题的序号）
设函数f（x）=tan（ωx+?），（ω＞0），条件P：“f（0）=0”；条件Q：“f（x）为奇函数”，则P是Q的（　　）
（2012•南京二模）下列四个命题
①“?x∈R，x2-x+1≤1”的否定；
②“若x2+x-6≥0，则x＞2”的否命题；
③在△ABC中，“A＞30°“sinA＞
12
”的充分不必要条件；
④“函数f（x）=tan（x+φ）为奇函数”的充要条件是“φ=kπ（k∈z）”．
其中真命题的序号是
②
②
．（把真命题的序号都填上）
已知函数f（x）=tan（2x+
π
4
）
（I）求该函数的定义域，周期及单调区间；
（II）若f（θ）=
1
7
，求
2cos2
θ
2
-sinθ-1
2
sin(θ+
π
4
)
的值．
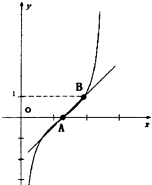精英家教网如图为函数f（x）=tan（
π
4
x-
π
2
）的部分图象，点A为函数f（x）在y轴右侧的第一个零点，点B在函数f（x）图象上，它的纵坐标为1，直线AB的倾斜角等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网