题目内容
已知双曲线与椭圆| x2 |
| 36 |
| y2 |
| 49 |
| 3 |
| 7 |
分析:由双曲线与椭圆
+
=1有公共的焦点,我们可以确定双曲线焦点的坐标,又由椭圆的离心率与双曲线的离心率之比为
,可以求出双曲线的离心率,进而求出双曲线的方程.
| x2 |
| 36 |
| y2 |
| 49 |
| 3 |
| 7 |
解答:解:双曲线焦点为(0,±
),设方程为
-
=1(a>0,b>0),
又椭圆离心率为
,设双曲线离心率e
∴
=
?e=
∴a=3,b2=4
∴双曲线方程为
-
=1
| 13 |
| y2 |
| a2 |
| x2 |
| b2 |
又椭圆离心率为
| ||
| 7 |
∴
| ||||
| e |
| 3 |
| 7 |
| ||
| 3 |
∴a=3,b2=4
∴双曲线方程为
| y2 |
| 9 |
| x2 |
| 4 |
点评:本题考查的知识点是椭圆及双曲线的性质,其中根据椭圆的标准方程,求出椭圆的焦点坐标及离心率,进而根据已知求出双曲线的焦点坐标及离心率是解答本题的关键.

练习册系列答案
相关题目
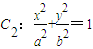 有公共焦点F1F2,点
有公共焦点F1F2,点 是它们的一个公共点.
是它们的一个公共点.