题目内容
如图,某商业中心O有通往正东方向和北偏东30方向的两条街道,某公园P位于商业中心北偏东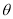 角(
角(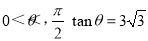 ),且与商业中心O的距离为
),且与商业中心O的距离为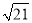 公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
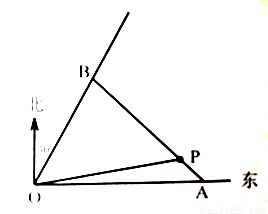
(1)当AB沿正北方向时,试求商业中心到A,B两处的距离和;
(2)若要使商业中心O到A,B两处的距离和最短,请确定A,B的最佳位置。
(1)13.5km.(2)商业中心到A、B两处的距离和最短为9km,此时OA=6km,OB=3km
【解析】
试题分析:(1)建立直角坐标系表示图中各量关系是解题关键: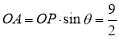 ,OB=2OA=9,商业中心到A、B两处的距离和为13.5km.(2)当AB与
,OB=2OA=9,商业中心到A、B两处的距离和为13.5km.(2)当AB与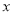 轴不垂直时,设AB:
轴不垂直时,设AB: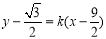 ,则
,则 ,又直线OB的方程为
,又直线OB的方程为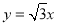 ,所以
,所以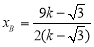 ,
, ,从而
,从而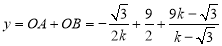 ,其中
,其中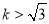 ,或
,或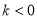 .利用导数可得当
.利用导数可得当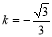 时,
时,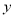 有极小值也是最小值为9km;此时OA=6km,OB=3km,
有极小值也是最小值为9km;此时OA=6km,OB=3km,
试题解析:

(1)以O为原点,OA所在直线为 轴建立坐标系.设
轴建立坐标系.设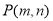 ,
,
∵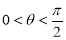 ,
,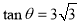 ∴
∴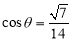 ,
,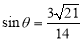 ,
,
则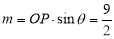 ,
, , 4分
, 4分
依题意,AB⊥OA,则OA=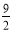 ,OB=2OA=9,商业中心到A、B两处的距离和为13.5km. 7分
,OB=2OA=9,商业中心到A、B两处的距离和为13.5km. 7分
(2)
方法1:当AB与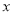 轴不垂直时,设AB:
轴不垂直时,设AB: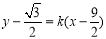 ,①
,①
令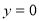 ,得
,得 ;由题意,直线OB的方程为
;由题意,直线OB的方程为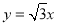 ,②
,②
解①②联立的方程组,得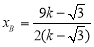 ,∴
,∴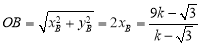 ,
,
∴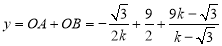 ,由
,由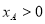 ,
,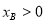 ,得
,得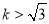 ,或
,或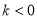 . 11分
. 11分
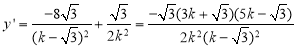 ,令
,令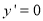 ,得
,得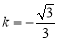 ,
,
当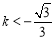 时,
时,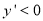 ,
,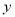 是减函数;当
是减函数;当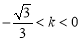 时,
时,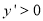 ,
,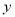 是增函数,
是增函数,
∴当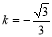 时,
时,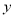 有极小值为9km;当
有极小值为9km;当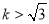 时,
时,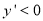 ,
,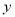 是减函数,结合(1)知
是减函数,结合(1)知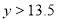 km.
km.
综上所述,商业中心到A、B两处的距离和最短为9km,此时OA=6km,OB=3km,
方法2:如图,过P作PM//OA交OB于M,PN//OB交OA于N,设∠BAO=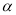 ,
,

△OPN中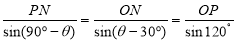 ,得PN=1,ON=4=PM,
,得PN=1,ON=4=PM,
△PNA中∠NPA=120°-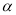 ∴
∴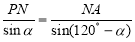 得
得
同理在△PMB中,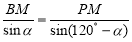 ,得
,得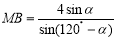 ,
,
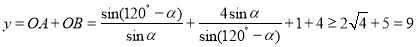 , 13分
, 13分
当且仅当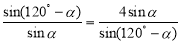 即
即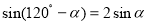 即
即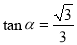 时取等号.
时取等号.
方法3:若设点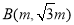 ,则AB:
,则AB: ,得
,得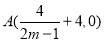 ,
,
∴ , 13分
, 13分
当且仅当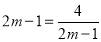 即
即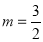 时取等号.
时取等号.
方法4:设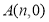 ,AB:
,AB: ,得
,得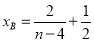 ,
,
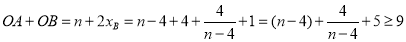 , 13分
, 13分
当且仅当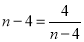 即
即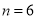 时取等号.
时取等号.
答:A选地址离商业中心6km,B离商业中心3km为最佳位置. 15分
考点:函数解析式,利用导数求最值
考点分析: 考点1:三角形的解的情况 考点2:解三角形 试题属性- 题型:
- 难度:
- 考核:
- 年级:

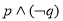 为假,则一定是p假q真
为假,则一定是p假q真 ”的否定是“
”的否定是“ 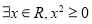 ”
”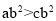 ”的充分不必要条件是“a>c”
”的充分不必要条件是“a>c”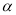 是一平面,a,b是两条不同的直线,若
是一平面,a,b是两条不同的直线,若 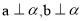 ,则a//b
,则a//b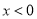 ”是“
”是“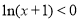 ”的( )
”的( ) 中,
中, ,
, ,
, ,
, ,
, 为
为 的三等分点,则
的三等分点,则 ( )
( ) B.
B. C.
C. D.
D.
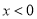 ”是“
”是“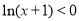 ”的( )
”的( ) }的前n项和为Sn,且
}的前n项和为Sn,且 ,若对任意
,若对任意 ,都有
,都有 ,则实数p的取值范围是
,则实数p的取值范围是

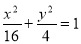 上的两点
上的两点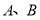 关于直线
关于直线 对称,则弦
对称,则弦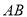 的中点坐标为( )
的中点坐标为( )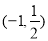 B.
B.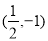 C.
C.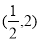 D.
D.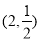
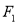 、
、 分别是双曲线
分别是双曲线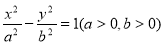 的两个焦点,以坐标原点
的两个焦点,以坐标原点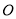 为圆心,
为圆心,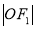 为半径的圆与该双曲线左支交于
为半径的圆与该双曲线左支交于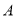 、
、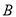 两点,若△
两点,若△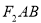 是等边三角形,则双曲线的离心率为 ( )
是等边三角形,则双曲线的离心率为 ( )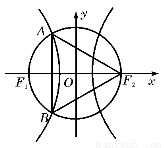
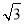 B.2 C.
B.2 C.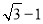 D.
D.