题目内容
已知向量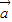 、
、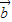 、
、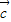 、
、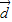 及实数x、y满足
及实数x、y满足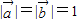 ,
,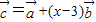 ,
, ,若
,若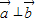 ,
,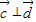 且
且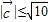 .
.(1)求y关于x的函数关系式y=f(x)及其定义域;
(2)若x∈[1,2]时,不等式f(x)≥mx-16恒成立,求实数m的取值范围.
【答案】分析:(1)由 ,知
,知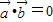 ,由
,由 ,知
,知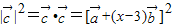 =1+(x-3)2,由此能求出y关于x的函数关系式y=f(x)及其定义域.
=1+(x-3)2,由此能求出y关于x的函数关系式y=f(x)及其定义域.
(2)当1≤x≤2时,欲使f(x)≥mx-16恒成立,即m≤x+ -3恒成立,由此能求出实数m的取值范围.
-3恒成立,由此能求出实数m的取值范围.
解答:解:(1)∵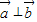 ,
,
∴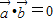 ,
,
又 ,
,
∴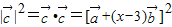 =1+(x-3)2,
=1+(x-3)2,
∵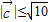 ,
,
∴1+(x-3)2≤10,解得0≤x≤6,
又∵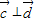 ,∴
,∴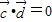 ,
,
而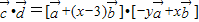 =-y+x(x-3),
=-y+x(x-3),
∴-y+x(x-3)=0,
∴y=f(x)=x(x-3),其定义域为[0,6].
(2)当1≤x≤2时,
欲使f(x)≥mx-16恒成立,
即使x2-3x≥mx-16恒成立,
∴mx≤x2-3x+16,
即m≤x+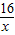 -3恒成立,
-3恒成立,
令g(x)=x+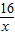 ,
,
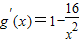 ,
,
当1≤x≤2时,g′(x)<0,
∴g(x)=x+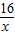 是减函数,
是减函数,
∴[g(x)]min=g(2)=2+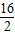 =10,
=10,
∴m≤x+ -3≤10-3=7
-3≤10-3=7
∴m≤7.
点评:本题考查平面向量的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
 ,知
,知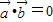 ,由
,由 ,知
,知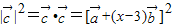 =1+(x-3)2,由此能求出y关于x的函数关系式y=f(x)及其定义域.
=1+(x-3)2,由此能求出y关于x的函数关系式y=f(x)及其定义域.(2)当1≤x≤2时,欲使f(x)≥mx-16恒成立,即m≤x+
 -3恒成立,由此能求出实数m的取值范围.
-3恒成立,由此能求出实数m的取值范围.解答:解:(1)∵
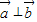 ,
,∴
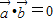 ,
,又
 ,
,∴
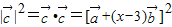 =1+(x-3)2,
=1+(x-3)2,∵
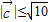 ,
,∴1+(x-3)2≤10,解得0≤x≤6,
又∵
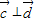 ,∴
,∴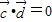 ,
,而
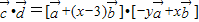 =-y+x(x-3),
=-y+x(x-3),∴-y+x(x-3)=0,
∴y=f(x)=x(x-3),其定义域为[0,6].
(2)当1≤x≤2时,
欲使f(x)≥mx-16恒成立,
即使x2-3x≥mx-16恒成立,
∴mx≤x2-3x+16,
即m≤x+
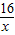 -3恒成立,
-3恒成立,令g(x)=x+
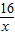 ,
,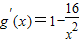 ,
,当1≤x≤2时,g′(x)<0,
∴g(x)=x+
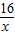 是减函数,
是减函数,∴[g(x)]min=g(2)=2+
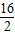 =10,
=10,∴m≤x+
 -3≤10-3=7
-3≤10-3=7∴m≤7.
点评:本题考查平面向量的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
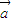 ,
, ,
,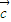 ,
, 及实数x,y且|
及实数x,y且|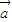 |=|
|=| |=1,
|=1, =
= +(x2-3)x
+(x2-3)x ,
,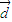 =-y
=-y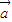 +
+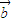 ,
,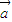 ⊥
⊥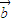 ,
, ⊥
⊥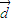 .
.